Hvordan beregne en andregradsligning. Løse kvadratiske ligninger ved hjelp av en diskriminant
I Moderne samfunn Evnen til å utføre operasjoner med ligninger som inneholder en variabel i kvadrat kan være nyttig innen mange aktivitetsområder og er mye brukt i praksis i vitenskapelig og teknisk utvikling. Bevis på dette kan finnes i utformingen av sjø- og elvefartøyer, fly og missiler. Ved hjelp av slike beregninger, banene for bevegelse av de fleste forskjellige kropper, gjelder også romobjekter. Eksempler med løsning av kvadratiske ligninger brukes ikke bare i økonomisk prognoser, i design og konstruksjon av bygninger, men også i de mest vanlige hverdagslige omstendigheter. De kan være nødvendige på fotturer, på sportsbegivenheter, i butikker ved kjøp og i andre svært vanlige situasjoner.
La oss dele uttrykket inn i dets komponentfaktorer
Graden av ligningen bestemmes maksimal verdi grad av variabelen som dette uttrykket inneholder. Hvis den er lik 2, kalles en slik ligning kvadratisk.
Hvis vi snakker på formlerspråket, kan de angitte uttrykkene, uansett hvordan de ser ut, alltid bringes til formen når venstre side av uttrykket består av tre ledd. Blant dem: akse 2 (det vil si en variabel kvadratisk med koeffisienten), bx (en ukjent uten kvadrat med koeffisienten) og c (en fri komponent, det vil si et vanlig tall). Alt dette på høyre side er lik 0. I tilfellet når et slikt polynom mangler en av sine konstituerende ledd, med unntak av akse 2, kalles det en ufullstendig andregradsligning. Eksempler med løsning av slike problemer, verdiene til variablene som er enkle å finne, bør vurderes først.
Hvis uttrykket ser ut som det har to ledd på høyre side, nærmere bestemt ax 2 og bx, er den enkleste måten å finne x ved å sette variabelen ut av parentes. Nå vil ligningen vår se slik ut: x(ax+b). Deretter blir det åpenbart at enten x=0, eller problemet kommer ned til å finne en variabel fra følgende uttrykk: ax+b=0. Dette er diktert av en av egenskapene til multiplikasjon. Regelen sier at produktet av to faktorer gir 0 bare hvis en av dem er null.
Eksempel
x=0 eller 8x - 3 = 0
Som et resultat får vi to røtter av ligningen: 0 og 0,375.
Ligninger av denne typen kan beskrive bevegelsen til kropper under påvirkning av tyngdekraften, som begynte å bevege seg fra et bestemt punkt tatt som opprinnelsen til koordinatene. Her har den matematiske notasjonen følgende form: y = v 0 t + gt 2 /2. Ved å erstatte de nødvendige verdiene, likestille høyresiden med 0 og finne mulige ukjente, kan du finne ut tiden som går fra det øyeblikket kroppen reiser seg til det øyeblikket den faller, samt mange andre størrelser. Men vi skal snakke om dette senere.

Faktorering av et uttrykk
Regelen beskrevet ovenfor gjør det mulig å løse disse problemene i mer komplekse saker. La oss se på eksempler på løsning av andregradsligninger av denne typen.
X 2 - 33x + 200 = 0
Dette kvadratiske trinomialet er komplett. La oss først transformere uttrykket og faktorisere det. Det er to av dem: (x-8) og (x-25) = 0. Som et resultat har vi to røtter 8 og 25.
Eksempler med å løse andregradsligninger i grad 9 lar denne metoden finne en variabel i uttrykk ikke bare av andre, men til og med av tredje og fjerde orden.
For eksempel: 2x 3 + 2x 2 - 18x - 18 = 0. Når du faktoriserer høyre side inn i faktorer med en variabel, er det tre av dem, det vil si (x+1), (x-3) og (x+ 3).
Som et resultat blir det åpenbart at denne ligningen har tre røtter: -3; -1; 3.
Kvadratrot
Et annet tilfelle av en ufullstendig andreordens ligning er et uttrykk representert i bokstavspråket på en slik måte at høyresiden er konstruert av komponentene akse 2 og c. Her, for å få verdien av variabelen, overføres frileddet til høyre side, og deretter trekkes kvadratroten ut fra begge sider av likheten. Det skal bemerkes at i i dette tilfellet Det er vanligvis to røtter til ligningen. De eneste unntakene kan være likheter som ikke inneholder et ledd med i det hele tatt, hvor variabelen er lik null, samt varianter av uttrykk når høyresiden er negativ. I sistnevnte tilfelle er det ingen løsninger i det hele tatt, siden handlingene ovenfor ikke kan utføres med røtter. Eksempler på løsninger på andregradsligninger av denne typen bør vurderes.
I dette tilfellet vil røttene til ligningen være tallene -4 og 4.
Beregning av landareal
Behovet for denne typen beregninger dukket opp i eldgamle tider, fordi utviklingen av matematikk i disse fjerne tider i stor grad ble bestemt av behovet for å bestemme med størst nøyaktighet arealene og omkretsene til tomter.

Vi bør også vurdere eksempler på løsning av andregradsligninger basert på problemer av denne typen.
Så la oss si at det er en rektangulær tomt, hvis lengde er 16 meter større enn bredden. Du bør finne lengden, bredden og omkretsen av stedet hvis du vet at området er 612 m2.
For å komme i gang, la oss først lage den nødvendige ligningen. La oss angi bredden på området med x, da vil lengden være (x+16). Av det som er skrevet følger det at arealet er bestemt av uttrykket x(x+16), som i henhold til betingelsene for vår oppgave er 612. Dette betyr at x(x+16) = 612.
Å løse komplette andregradsligninger, og dette uttrykket er akkurat det, kan ikke gjøres på samme måte. Hvorfor? Selv om venstre side fortsatt inneholder to faktorer, er deres produkt ikke lik 0 i det hele tatt, så forskjellige metoder brukes her.
Diskriminerende
Først av alt, la oss gjøre de nødvendige transformasjonene, da utseende av dette uttrykket vil se slik ut: x 2 + 16x - 612 = 0. Dette betyr at vi har fått et uttrykk i en form som tilsvarer den tidligere spesifiserte standarden, hvor a=1, b=16, c=-612.
Dette kan være et eksempel på å løse andregradsligninger ved hjelp av en diskriminant. Her nødvendige beregninger produseres i henhold til skjemaet: D = b 2 - 4ac. Denne hjelpemengden gjør det ikke bare mulig å finne de nødvendige mengdene i en andreordens ligning, den bestemmer mengden mulige alternativer. Hvis D>0, er det to av dem; for D=0 er det én rot. I tilfelle D<0, никаких шансов для решения у уравнения вообще не имеется.
Om røtter og deres formel
I vårt tilfelle er diskriminanten lik: 256 - 4(-612) = 2704. Dette tyder på at problemet vårt har et svar. Hvis du kjenner k, må løsningen av andregradsligninger fortsettes ved å bruke formelen nedenfor. Den lar deg beregne røttene.

Dette betyr at i det presenterte tilfellet: x 1 =18, x 2 =-34. Det andre alternativet i dette dilemmaet kan ikke være en løsning, fordi dimensjonene til tomten ikke kan måles i negative mengder, noe som betyr at x (det vil si bredden på tomten) er 18 m. Herfra beregner vi lengden: 18 +16=34, og omkretsen 2(34+ 18)=104(m2).
Eksempler og oppgaver
Vi fortsetter vår studie av kvadratiske ligninger. Eksempler og detaljerte løsninger på flere av dem vil bli gitt nedenfor.
1) 15x 2 + 20x + 5 = 12x 2 + 27x + 1
La oss flytte alt til venstre side av likheten, gjøre en transformasjon, det vil si at vi får den typen ligning som vanligvis kalles standard, og likestille den til null.
15x 2 + 20x + 5 - 12x 2 - 27x - 1 = 0
Ved å legge til lignende, bestemmer vi diskriminanten: D = 49 - 48 = 1. Dette betyr at ligningen vår vil ha to røtter. La oss beregne dem i henhold til formelen ovenfor, noe som betyr at den første av dem vil være lik 4/3, og den andre til 1.
2) La oss nå løse mysterier av et annet slag.
La oss finne ut om det er noen røtter her x 2 - 4x + 5 = 1? For å få et omfattende svar, la oss redusere polynomet til den tilsvarende vanlige formen og beregne diskriminanten. I eksemplet ovenfor, løsningen kvadratisk ligning det er ikke nødvendig å produsere, for det er slett ikke essensen av oppgaven. I dette tilfellet er D = 16 - 20 = -4, som betyr at det egentlig ikke er noen røtter.
Vietas teorem
Det er praktisk å løse kvadratiske ligninger ved å bruke formlene ovenfor og diskriminanten, når kvadratroten er tatt fra verdien av sistnevnte. Men dette skjer ikke alltid. Imidlertid er det mange måter å få verdiene til variabler på i dette tilfellet. Eksempel: løse andregradsligninger ved å bruke Vietas teorem. Hun er oppkalt etter som levde på 1500-tallet i Frankrike og gjorde en strålende karriere takket være hans matematiske talent og forbindelser ved hoffet. Portrettet hans kan sees i artikkelen.

Mønsteret som den berømte franskmannen la merke til var som følger. Han beviste at røttene til ligningen summerer seg numerisk til -p=b/a, og deres produkt tilsvarer q=c/a.
La oss nå se på spesifikke oppgaver.
3x 2 + 21x - 54 = 0
For enkelhets skyld, la oss transformere uttrykket:
x 2 + 7x - 18 = 0
La oss bruke Vietas teorem, dette vil gi oss følgende: summen av røttene er -7, og deres produkt er -18. Herfra får vi at røttene til ligningen er tallene -9 og 2. Etter å ha sjekket vil vi forsikre oss om at disse variabelverdiene virkelig passer inn i uttrykket.
Parabelgraf og ligning
Begrepene kvadratisk funksjon og andregradsligninger er nært beslektet. Eksempler på dette er allerede gitt tidligere. La oss nå se litt mer detaljert på noen matematiske gåter. Enhver ligning av den beskrevne typen kan representeres visuelt. Et slikt forhold, tegnet som en graf, kalles en parabel. De forskjellige typene er presentert i figuren nedenfor.

Enhver parabel har et toppunkt, det vil si et punkt der grenene kommer ut. Hvis a>0, går de høyt til uendelig, og når a<0, они рисуются вниз. Простейшим примером подобной зависимости является функция y = x 2 . В данном случае в уравнении x 2 =0 неизвестное может принимать только одно значение, то есть х=0, а значит существует только один корень. Это неудивительно, ведь здесь D=0, потому что a=1, b=0, c=0. Выходит формула корней (точнее одного корня) квадратного уравнения запишется так: x = -b/2a.
Visuelle representasjoner av funksjoner hjelper til med å løse alle ligninger, inkludert kvadratiske. Denne metoden kalles grafisk. Og verdien av x-variabelen er abscissekoordinaten i punktene der graflinjen skjærer 0x. Koordinatene til toppunktet kan bli funnet ved å bruke formelen som nettopp er gitt x 0 = -b/2a. Og ved å erstatte den resulterende verdien i den opprinnelige ligningen til funksjonen, kan du finne ut y 0, det vil si den andre koordinaten til toppunktet til parabelen, som tilhører ordinataksen.
Skjæringspunktet mellom grenene til en parabel med abscisseaksen
Det finnes mange eksempler på løsning av kvadratiske ligninger, men det er også generelle mønstre. La oss se på dem. Det er klart at skjæringspunktet mellom grafen og 0x-aksen for a>0 bare er mulig hvis y 0 tar negative verdier. Og for en<0 координата у 0 должна быть положительна. Для указанных вариантов D>0. Ellers D<0. А когда D=0, вершина параболы расположена непосредственно на оси 0х.
Fra grafen til parablen kan du også bestemme røttene. Det motsatte er også sant. Det vil si at hvis det ikke er lett å få en visuell representasjon av en kvadratisk funksjon, kan du likestille høyre side av uttrykket til 0 og løse den resulterende ligningen. Og når man kjenner skjæringspunktene med 0x-aksen, er det lettere å konstruere en graf.
Fra historien
Ved å bruke ligninger som inneholder en kvadratisk variabel, gjorde de i gamle dager ikke bare matematiske beregninger og bestemte arealene til geometriske figurer. De gamle trengte slike beregninger for store funn innen fysikk og astronomi, samt for å lage astrologiske prognoser.

Som moderne vitenskapsmenn foreslår, var innbyggerne i Babylon blant de første som løste kvadratiske ligninger. Dette skjedde fire århundrer før vår tidsregning. Selvfølgelig var deres beregninger radikalt forskjellige fra de som for tiden er akseptert og viste seg å være mye mer primitive. For eksempel hadde mesopotamiske matematikere ingen anelse om eksistensen av negative tall. De var også ukjente med andre finesser som ethvert moderne skolebarn kjenner til.
Kanskje enda tidligere enn forskerne i Babylon begynte vismannen fra India Baudhayama å løse kvadratiske ligninger. Dette skjedde omtrent åtte århundrer før Kristi æra. Riktignok var andreordensligningene, metodene for å løse som han ga, de enkleste. Foruten ham var kinesiske matematikere også interessert i lignende spørsmål i gamle dager. I Europa begynte kvadratiske ligninger å bli løst først på begynnelsen av 1200-tallet, men senere ble de brukt i deres arbeider av så store forskere som Newton, Descartes og mange andre.
For å fortsette med emnet "Løse ligninger", vil materialet i denne artikkelen introdusere deg til kvadratiske ligninger.
La oss se på alt i detalj: essensen og notasjonen til en kvadratisk ligning, definere de medfølgende begrepene, analysere skjemaet for å løse ufullstendige og fullstendige ligninger, bli kjent med formelen for røtter og diskriminanten, etablere forbindelser mellom røttene og koeffisientene, og selvfølgelig vil vi gi en visuell løsning på praktiske eksempler.
Yandex.RTB R-A-339285-1
Kvadratisk ligning, dens typer
Definisjon 1Kvadratisk ligning er en ligning skrevet som a x 2 + b x + c = 0, Hvor x– variabel, a , b og c– noen tall, mens en er ikke null.
Ofte kalles andregradsligninger også andregradsligninger, siden en andregradsligning i hovedsak er en algebraisk ligning av andre grad.
La oss gi et eksempel for å illustrere den gitte definisjonen: 9 x 2 + 16 x + 2 = 0 ; 7, 5 x 2 + 3, 1 x + 0, 11 = 0, osv. Dette er andregradsligninger.
Definisjon 2
Tallene a, b og c er koeffisientene til den kvadratiske ligningen a x 2 + b x + c = 0, mens koeffisienten en kalles den første, eller senior, eller koeffisient ved x 2, b - den andre koeffisienten, eller koeffisient ved x, A c kalt et gratis medlem.
For eksempel i andregradsligningen 6 x 2 − 2 x − 11 = 0 den ledende koeffisienten er 6, den andre koeffisienten er − 2 , og fritiden er lik − 11 . La oss ta hensyn til det faktum at når koeffisientene b og/eller c er negative, så brukes en kortform av formen 6 x 2 − 2 x − 11 = 0, men ikke 6 x 2 + (− 2) x + (− 11) = 0.
La oss også avklare dette aspektet: hvis koeffisientene en og/eller b lik 1 eller − 1 , så tar de kanskje ikke en eksplisitt del i å skrive kvadratisk ligning, som forklares av særegenhetene ved å skrive de angitte numeriske koeffisientene. For eksempel i andregradsligningen y 2 − y + 7 = 0 den ledende koeffisienten er 1, og den andre koeffisienten er − 1 .
Reduserte og ureduserte kvadratiske ligninger
Basert på verdien av den første koeffisienten deles kvadratiske ligninger inn i redusert og uredusert.
Definisjon 3
Redusert andregradsligning er en kvadratisk ligning der den ledende koeffisienten er 1. For andre verdier av den ledende koeffisienten er kvadratisk ligning ikke-redusert.
La oss gi eksempler: kvadratiske ligninger x 2 − 4 · x + 3 = 0, x 2 − x − 4 5 = 0 reduseres, i hver av dem er den ledende koeffisienten 1.
9 x 2 − x − 2 = 0- uredusert kvadratisk ligning, hvor den første koeffisienten er forskjellig fra 1 .
Enhver ikke-redusert kvadratisk ligning kan konverteres til en redusert ligning ved å dele begge sider med den første koeffisienten (ekvivalent transformasjon). Den transformerte ligningen vil ha de samme røttene som den gitte, ikke-reduserte ligningen eller vil heller ikke ha noen røtter i det hele tatt.
Betraktning av et spesifikt eksempel vil tillate oss å tydelig demonstrere overgangen fra en ikke-redusert kvadratisk ligning til en redusert.
Eksempel 1
Gitt ligningen 6 x 2 + 18 x − 7 = 0 . Det er nødvendig å konvertere den opprinnelige ligningen til den reduserte formen.
Løsning
I henhold til skjemaet ovenfor deler vi begge sider av den opprinnelige ligningen med ledende koeffisient 6. Da får vi: (6 x 2 + 18 x − 7): 3 = 0: 3, og dette er det samme som: (6 x 2) : 3 + (18 x) : 3 − 7: 3 = 0 og videre: (6: 6) x 2 + (18: 6) x − 7: 6 = 0. Herfra: x 2 + 3 x - 1 1 6 = 0. Dermed oppnås en ligning tilsvarende den gitte.
Svar: x 2 + 3 x - 1 1 6 = 0.
Fullstendige og ufullstendige andregradsligninger
La oss gå til definisjonen av en kvadratisk ligning. I den spesifiserte vi det a ≠ 0. En lignende betingelse er nødvendig for ligningen a x 2 + b x + c = 0 var nettopp firkantet, siden kl a = 0 det forvandles i hovedsak til lineær ligning b x + c = 0.
I tilfellet når koeffisientene b Og c er lik null (noe som er mulig, både individuelt og sammen), kalles andregradsligningen ufullstendig.
Definisjon 4
Ufullstendig andregradsligning- en slik andregradsligning a x 2 + b x + c = 0, hvor minst én av koeffisientene b Og c(eller begge) er null.
Fullfør andregradsligningen– en kvadratisk ligning der alle numeriske koeffisienter ikke er lik null.
La oss diskutere hvorfor typene kvadratiske ligninger gis akkurat disse navnene.
Når b = 0, tar andregradsligningen formen a x 2 + 0 x + c = 0, som er det samme som a x 2 + c = 0. På c = 0 andregradsligningen skrives som a x 2 + b x + 0 = 0, som tilsvarer a x 2 + b x = 0. På b = 0 Og c = 0 ligningen vil ta formen a x 2 = 0. Ligningene som vi fikk, skiller seg fra den komplette andregradslikningen ved at venstresiden deres ikke inneholder verken et ledd med variabelen x, eller et fritt ledd, eller begge deler. Faktisk ga dette faktum navnet til denne typen ligninger - ufullstendig.
For eksempel er x 2 + 3 x + 4 = 0 og − 7 x 2 − 2 x + 1, 3 = 0 komplette andregradsligninger; x 2 = 0, − 5 x 2 = 0; 11 x 2 + 2 = 0, − x 2 − 6 x = 0 – ufullstendige andregradsligninger.
Løse ufullstendige andregradsligninger
Definisjonen gitt ovenfor gjør det mulig å skille mellom følgende typer ufullstendige kvadratiske ligninger:
- a x 2 = 0, tilsvarer denne ligningen koeffisientene b = 0 og c = 0;
- a · x 2 + c = 0 ved b = 0;
- a · x 2 + b · x = 0 ved c = 0.
La oss vurdere sekvensielt løsningen av hver type ufullstendig kvadratisk ligning.
Løsning av ligningen a x 2 =0
Som nevnt ovenfor tilsvarer denne ligningen koeffisientene b Og c, lik null. Ligningen a x 2 = 0 kan konverteres til en ekvivalent ligning x 2 = 0, som vi får ved å dele begge sider av den opprinnelige ligningen med tallet en, ikke lik null. Det åpenbare faktum er at roten til ligningen x 2 = 0 dette er null fordi 0 2 = 0 . Denne ligningen har ingen andre røtter, noe som kan forklares med egenskapene til graden: for et hvilket som helst tall p, ikke lik null, er ulikheten sann p 2 > 0, hvorav det følger at når p ≠ 0 likestilling p 2 = 0 vil aldri bli oppnådd.
Definisjon 5
For den ufullstendige andregradsligningen a x 2 = 0 er det altså en unik rot x = 0.
Eksempel 2
La oss for eksempel løse en ufullstendig andregradsligning − 3 x 2 = 0. Det tilsvarer ligningen x 2 = 0, dens eneste rot er x = 0, så har den opprinnelige ligningen en enkelt rot - null.
Kort fortalt er løsningen skrevet som følger:
− 3 x 2 = 0, x 2 = 0, x = 0.
Løse ligningen a x 2 + c = 0
Neste i rekken er løsningen av ufullstendige andregradsligninger, der b = 0, c ≠ 0, det vil si ligninger av formen a x 2 + c = 0. La oss transformere denne ligningen ved å flytte et ledd fra den ene siden av ligningen til den andre, endre tegnet til det motsatte og dele begge sider av ligningen med et tall som ikke er lik null:
- overføre c til høyre side, som gir ligningen a x 2 = − c;
- del begge sider av ligningen med en, vi ender opp med x = - c a .
Våre transformasjoner er tilsvarende, den resulterende ligningen er også ekvivalent med den opprinnelige, og dette faktum gjør det mulig å trekke konklusjoner om røttene til ligningen. Fra hva verdiene er en Og c verdien av uttrykket - c a avhenger: det kan ha et minustegn (for eksempel if a = 1 Og c = 2, deretter - c a = - 2 1 = - 2) eller et plusstegn (for eksempel if a = − 2 Og c = 6 så - c a = - 6 - 2 = 3); det er ikke null fordi c ≠ 0. La oss dvele mer detaljert ved situasjoner når - ca< 0 и - c a > 0 .
I tilfelle når - c a< 0 , уравнение x 2 = - c a не будет иметь корней. Утверждая это, мы опираемся на то, что квадратом любого числа является число неотрицательное. Из сказанного следует, что при - c a < 0 ни для какого числа s likheten p 2 = - c a kan ikke være sann.
Alt er annerledes når - c a > 0: husk kvadratroten, og det vil bli tydelig at roten til ligningen x 2 = - c a vil være tallet - c a, siden - c a 2 = - c a. Det er ikke vanskelig å forstå at tallet - - c a også er roten til ligningen x 2 = - c a: ja, - - c a 2 = - c a.
Ligningen vil ikke ha andre røtter. Vi kan demonstrere dette ved å bruke metoden for selvmotsigelse. Til å begynne med, la oss definere notasjonene for røttene ovenfor som x 1 Og − x 1. La oss anta at likningen x 2 = - c a også har en rot x 2, som er forskjellig fra røttene x 1 Og − x 1. Vi vet det ved å substituere inn i ligningen x sine røtter transformerer vi ligningen til en rettferdig numerisk likhet.
Til x 1 Og − x 1 vi skriver: x 1 2 = - c a , og for x 2- x 2 2 = - c a . Basert på egenskapene til numeriske likheter, trekker vi et riktig likhetsledd for ledd fra et annet, noe som vil gi oss: x 1 2 − x 2 2 = 0. Vi bruker egenskapene til operasjoner med tall for å omskrive den siste likheten som (x 1 − x 2) · (x 1 + x 2) = 0. Det er kjent at produktet av to tall er null hvis og bare hvis minst ett av tallene er null. Av ovenstående følger det x 1 − x 2 = 0 og/eller x 1 + x 2 = 0, som er det samme x 2 = x 1 og/eller x 2 = − x 1. En åpenbar motsetning oppsto, fordi man først var enige om at roten til ligningen x 2 skiller seg fra x 1 Og − x 1. Så vi har bevist at ligningen ikke har andre røtter enn x = - c a og x = - - c a.
La oss oppsummere alle argumentene ovenfor.
Definisjon 6
Ufullstendig andregradsligning a x 2 + c = 0 er ekvivalent med ligningen x 2 = - c a, som:
- vil ikke ha røtter ved - c a< 0 ;
- vil ha to røtter x = - c a og x = - - c a for - c a > 0.
La oss gi eksempler på løsning av likningene a x 2 + c = 0.
Eksempel 3
Gitt en andregradsligning 9 x 2 + 7 = 0. Det er nødvendig å finne en løsning.
Løsning
La oss flytte frileddet til høyre side av ligningen, så vil ligningen ta formen 9 x 2 = − 7.
La oss dele begge sider av den resulterende ligningen med 9
, kommer vi til x 2 = - 7 9 . På høyre side ser vi et tall med et minustegn, som betyr: y gitt ligning ingen røtter. Deretter den opprinnelige ufullstendige andregradsligningen 9 x 2 + 7 = 0 vil ikke ha røtter.
Svar: ligningen 9 x 2 + 7 = 0 har ingen røtter.
Eksempel 4
Ligningen må løses − x 2 + 36 = 0.
Løsning
La oss flytte 36 til høyre side: − x 2 = − 36.
La oss dele begge deler med − 1
, vi får x 2 = 36. På høyre side er det et positivt tall, som vi kan konkludere med
x = 36 eller
x = -36.
La oss trekke ut roten og skrive ned det endelige resultatet: ufullstendig andregradsligning − x 2 + 36 = 0 har to røtter x = 6 eller x = − 6.
Svar: x = 6 eller x = − 6.
Løsning av ligningen a x 2 +b x=0
La oss analysere den tredje typen ufullstendige kvadratiske ligninger, når c = 0. Å finne en løsning på en ufullstendig andregradsligning a x 2 + b x = 0, vil vi bruke faktoriseringsmetoden. La oss faktorisere polynomet som er på venstre side av ligningen, og ta den felles faktoren ut av parentes x. Dette trinnet vil gjøre det mulig å transformere den opprinnelige ufullstendige kvadratiske ligningen til dens ekvivalent x (a x + b) = 0. Og denne ligningen tilsvarer i sin tur et sett med ligninger x = 0 Og a x + b = 0. Ligningen a x + b = 0 lineær, og dens rot: x = − b a.
Definisjon 7
Dermed den ufullstendige andregradsligningen a x 2 + b x = 0 vil ha to røtter x = 0 Og x = − b a.
La oss forsterke materialet med et eksempel.
Eksempel 5
Det er nødvendig å finne en løsning på ligningen 2 3 · x 2 - 2 2 7 · x = 0.
Løsning
Vi tar den ut x utenfor parentes får vi ligningen x · 2 3 · x - 2 2 7 = 0 . Denne ligningen er ekvivalent med ligningene x = 0 og 2 3 x - 2 2 7 = 0. Nå skal du løse den resulterende lineære ligningen: 2 3 · x = 2 2 7, x = 2 2 7 2 3.
Skriv kort løsningen til ligningen slik:
2 3 x 2 - 2 2 7 x = 0 x 2 3 x - 2 2 7 = 0
x = 0 eller 2 3 x - 2 2 7 = 0
x = 0 eller x = 3 3 7
Svar: x = 0, x = 3 3 7.
Diskriminant, formel for røttene til en andregradsligning
For å finne løsninger på kvadratiske ligninger, er det en rotformel:
Definisjon 8
x = - b ± D 2 · a, hvor D = b 2 − 4 a c– den såkalte diskriminanten til en kvadratisk ligning.
Å skrive x = - b ± D 2 · a betyr i hovedsak at x 1 = - b + D 2 · a, x 2 = - b - D 2 · a.
Det ville være nyttig å forstå hvordan denne formelen ble utledet og hvordan man bruker den.
Utledning av formelen for røttene til en andregradsligning
La oss stå overfor oppgaven med å løse en andregradsligning a x 2 + b x + c = 0. La oss utføre en rekke tilsvarende transformasjoner:
- del begge sider av ligningen med et tall en, forskjellig fra null, får vi følgende andregradsligning: x 2 + b a · x + c a = 0 ;
- La oss velge hele kvadratet på venstre side av den resulterende ligningen:
x 2 + b a · x + c a = x 2 + 2 · b 2 · a · x + b 2 · a 2 - b 2 · a 2 + c a = = x + b 2 · a 2 - b 2 · a 2 + c a
Etter dette vil ligningen ha formen: x + b 2 · a 2 - b 2 · a 2 + c a = 0; - Nå er det mulig å overføre de to siste leddene til høyre side, endre tegnet til det motsatte, hvoretter vi får: x + b 2 · a 2 = b 2 · a 2 - c a ;
- Til slutt transformerer vi uttrykket skrevet på høyre side av den siste likheten:
b 2 · a 2 - c a = b 2 4 · a 2 - c a = b 2 4 · a 2 - 4 · a · c 4 · a 2 = b 2 - 4 · a · c 4 · a 2 .
Dermed kommer vi frem til likningen x + b 2 · a 2 = b 2 - 4 · a · c 4 · a 2 , tilsvarende den opprinnelige likningen a x 2 + b x + c = 0.
Vi undersøkte løsningen av slike ligninger i de foregående avsnittene (løsning av ufullstendige kvadratiske ligninger). Erfaringene som allerede er oppnådd gjør det mulig å trekke en konklusjon om røttene til ligningen x + b 2 · a 2 = b 2 - 4 · a · c 4 · a 2:
- med b 2 - 4 a c 4 a 2< 0 уравнение не имеет действительных решений;
- når b 2 - 4 · a · c 4 · a 2 = 0, er ligningen x + b 2 · a 2 = 0, så er x + b 2 · a = 0.
Herfra er den eneste roten x = - b 2 · a åpenbar;
- for b 2 - 4 · a · c 4 · a 2 > 0, vil følgende være sant: x + b 2 · a = b 2 - 4 · a · c 4 · a 2 eller x = b 2 · a - b 2 - 4 · a · c 4 · a 2 , som er det samme som x + - b 2 · a = b 2 - 4 · a · c 4 · a 2 eller x = - b 2 · a - b 2 - 4 · a · c 4 · a 2 , dvs. ligningen har to røtter.
Det er mulig å konkludere med at tilstedeværelsen eller fraværet av røtter til ligningen x + b 2 · a 2 = b 2 - 4 · a · c 4 · a 2 (og derfor den opprinnelige ligningen) avhenger av tegnet til uttrykket b 2 - 4 · a · c 4 · a 2 skrevet på høyre side. Og tegnet på dette uttrykket er gitt av tegnet på telleren, (nevner 4 a 2 vil alltid være positiv), det vil si tegnet på uttrykket b 2 − 4 a c. Dette uttrykket b 2 − 4 a c navnet er gitt - diskriminanten til den kvadratiske ligningen og bokstaven D er definert som dens betegnelse. Her kan du skrive ned essensen av diskriminanten - basert på dens verdi og fortegn kan de konkludere om den andregradsligningen vil ha reelle røtter, og i så fall hva er antallet røtter - en eller to.
La oss gå tilbake til likningen x + b 2 · a 2 = b 2 - 4 · a · c 4 · a 2 . La oss omskrive det med diskriminantnotasjon: x + b 2 · a 2 = D 4 · a 2 .
La oss formulere våre konklusjoner igjen:
Definisjon 9
- på D< 0 ligningen har ingen reelle røtter;
- på D=0 ligningen har en enkelt rot x = - b 2 · a ;
- på D > 0 ligningen har to røtter: x = - b 2 · a + D 4 · a 2 eller x = - b 2 · a - D 4 · a 2. Basert på egenskapene til radikaler kan disse røttene skrives på formen: x = - b 2 · a + D 2 · a eller - b 2 · a - D 2 · a. Og når vi åpner modulene og bringer brøkene til en fellesnevner, får vi: x = - b + D 2 · a, x = - b - D 2 · a.
Så resultatet av resonnementet vårt var utledningen av formelen for røttene til en kvadratisk ligning:
x = - b + D2a, x = -b - D2a, diskriminant D beregnet med formelen D = b 2 − 4 a c.
Disse formlene gjør det mulig å bestemme begge reelle røtter når diskriminanten er større enn null. Når diskriminanten er null, vil bruk av begge formlene gi samme rot, som eneste beslutning kvadratisk ligning. I tilfellet hvor diskriminanten er negativ, hvis vi prøver å bruke formelen for roten til en kvadratisk ligning, vil vi stå overfor behovet for å trekke ut kvadratroten av negativt tall, som vil ta oss utover reelle tall. Med en negativ diskriminant vil den kvadratiske ligningen ikke ha reelle røtter, men et par komplekse konjugerte røtter er mulig, bestemt av de samme rotformlene vi fikk.
Algoritme for å løse andregradsligninger ved hjelp av rotformler
Det er mulig å løse en andregradsligning ved å umiddelbart bruke rotformelen, men dette gjøres vanligvis når det er nødvendig å finne komplekse røtter.
I de fleste tilfeller betyr det vanligvis ikke å søke etter komplekse, men etter reelle røtter til en kvadratisk ligning. Da er det optimalt, før du bruker formlene for røttene til en kvadratisk ligning, først å bestemme diskriminanten og sørge for at den ikke er negativ (ellers vil vi konkludere med at ligningen ikke har noen reelle røtter), og deretter fortsette med å beregne verdien av røttene.
Resonnementet ovenfor gjør det mulig å formulere en algoritme for å løse en andregradsligning.
Definisjon 10
For å løse en andregradsligning a x 2 + b x + c = 0, nødvendig:
- i henhold til formelen D = b 2 − 4 a c finne den diskriminerende verdien;
- hos D< 0 сделать вывод об отсутствии у квадратного уравнения действительных корней;
- for D = 0, finn den eneste roten av ligningen ved å bruke formelen x = - b 2 · a ;
- for D > 0, bestem to reelle røtter av kvadratisk ligning ved å bruke formelen x = - b ± D 2 · a.
Merk at når diskriminanten er null, kan du bruke formelen x = - b ± D 2 · a, det vil gi samme resultat som formelen x = - b 2 · a.
La oss se på eksempler.
Eksempler på løsning av andregradsligninger
La oss gi en løsning på eksemplene for forskjellige betydninger diskriminerende.
Eksempel 6
Vi må finne røttene til ligningen x 2 + 2 x − 6 = 0.
Løsning
La oss skrive ned de numeriske koeffisientene til den kvadratiske ligningen: a = 1, b = 2 og c = − 6. Deretter fortsetter vi i henhold til algoritmen, dvs. La oss begynne å beregne diskriminanten, som vi vil erstatte koeffisientene a, b Og c inn i diskriminantformelen: D = b 2 − 4 · a · c = 2 2 − 4 · 1 · (− 6) = 4 + 24 = 28 .
Så vi får D > 0, som betyr at den opprinnelige ligningen vil ha to reelle røtter.
For å finne dem bruker vi rotformelen x = - b ± D 2 · a, og erstatter de tilsvarende verdiene, får vi: x = - 2 ± 28 2 · 1. La oss forenkle det resulterende uttrykket ved å ta faktoren ut av rottegnet og deretter redusere brøken:
x = - 2 ± 2 7 2
x = - 2 + 2 7 2 eller x = - 2 - 2 7 2
x = - 1 + 7 eller x = - 1 - 7
Svar: x = - 1 + 7, x = - 1 - 7 .
Eksempel 7
Må løse en andregradsligning − 4 x 2 + 28 x − 49 = 0.
Løsning
La oss definere diskriminanten: D = 28 2 − 4 · (− 4) · (− 49) = 784 − 784 = 0. Med denne verdien av diskriminanten vil den opprinnelige ligningen bare ha én rot, bestemt av formelen x = - b 2 · a.
x = - 28 2 (- 4) x = 3,5
Svar: x = 3,5.
Eksempel 8
Ligningen må løses 5 y 2 + 6 y + 2 = 0
Løsning
De numeriske koeffisientene til denne ligningen vil være: a = 5, b = 6 og c = 2. Vi bruker disse verdiene for å finne diskriminanten: D = b 2 − 4 · a · c = 6 2 − 4 · 5 · 2 = 36 − 40 = − 4 . Den beregnede diskriminanten er negativ, så den opprinnelige kvadratiske ligningen har ingen reelle røtter.
I tilfellet når oppgaven er å indikere komplekse røtter, bruker vi rotformelen og utfører handlinger med komplekse tall:
x = - 6 ± - 4 2 5,
x = - 6 + 2 i 10 eller x = - 6 - 2 i 10,
x = - 3 5 + 1 5 · i eller x = - 3 5 - 1 5 · i.
Svar: det er ingen reelle røtter; de komplekse røttene er som følger: - 3 5 + 1 5 · i, - 3 5 - 1 5 · i.
I skolepensum Det er ingen standardkrav for å lete etter komplekse røtter, derfor, hvis diskriminanten under løsningen blir bestemt til å være negativ, blir svaret umiddelbart skrevet ned at det ikke er noen reelle røtter.
Rotformel for selv andre koeffisienter
Rotformelen x = - b ± D 2 · a (D = b 2 − 4 · a · c) gjør det mulig å oppnå en annen formel, mer kompakt, slik at man kan finne løsninger på kvadratiske ligninger med en jevn koeffisient for x ( eller med en koeffisient på formen 2 · n, for eksempel 2 3 eller 14 ln 5 = 2 7 ln 5). La oss vise hvordan denne formelen er utledet.
La oss stå overfor oppgaven med å finne en løsning på den kvadratiske ligningen a · x 2 + 2 · n · x + c = 0 . Vi fortsetter i henhold til algoritmen: vi bestemmer diskriminanten D = (2 n) 2 − 4 a c = 4 n 2 − 4 a c = 4 (n 2 − a c), og bruker deretter rotformelen:
x = - 2 n ± D 2 a, x = - 2 n ± 4 n 2 - a c 2 a, x = - 2 n ± 2 n 2 - a c 2 a, x = - n ± n 2 - a · c a.
La uttrykket n 2 − a · c betegnes som D 1 (noen ganger er det betegnet D "). Da vil formelen for røttene til den andregradsligningen som vurderes med den andre koeffisienten 2 · n ha formen:
x = - n ± D 1 a, hvor D 1 = n 2 − a · c.
Det er lett å se at D = 4 · D 1, eller D 1 = D 4. D 1 er med andre ord en fjerdedel av diskriminanten. Tydeligvis er tegnet på D 1 det samme som tegnet på D, noe som betyr at tegnet på D 1 også kan tjene som en indikator på tilstedeværelsen eller fraværet av røttene til en kvadratisk ligning.
Definisjon 11
For å finne en løsning på en kvadratisk ligning med en andre koeffisient på 2 n, er det nødvendig:
- finn D 1 = n 2 − a · c ;
- på D 1< 0 сделать вывод, что действительных корней нет;
- når D 1 = 0, bestem den eneste roten av ligningen ved å bruke formelen x = - n a;
- for D 1 > 0, bestem to reelle røtter ved å bruke formelen x = - n ± D 1 a.
Eksempel 9
Det er nødvendig å løse den kvadratiske ligningen 5 x 2 − 6 x − 32 = 0.
Løsning
Vi kan representere den andre koeffisienten til den gitte ligningen som 2 · (− 3) . Deretter omskriver vi den gitte andregradsligningen til 5 x 2 + 2 (− 3) x − 32 = 0, hvor a = 5, n = − 3 og c = − 32.
La oss beregne den fjerde delen av diskriminanten: D 1 = n 2 − a · c = (− 3) 2 − 5 · (− 32) = 9 + 160 = 169. Den resulterende verdien er positiv, noe som betyr at ligningen har to reelle røtter. La oss bestemme dem ved å bruke den tilsvarende rotformelen:
x = - n ± D 1 a, x = - - 3 ± 169 5, x = 3 ± 13 5,
x = 3 + 13 5 eller x = 3 - 13 5
x = 3 1 5 eller x = - 2
Det ville være mulig å utføre beregninger ved å bruke den vanlige formelen for røttene til en kvadratisk ligning, men i dette tilfellet vil løsningen være mer tungvint.
Svar: x = 3 1 5 eller x = - 2 .
Forenkle formen til kvadratiske ligninger
Noen ganger er det mulig å optimalisere formen til den opprinnelige ligningen, noe som vil forenkle prosessen med å beregne røttene.
For eksempel er den andregradsligningen 12 x 2 − 4 x − 7 = 0 klart mer praktisk å løse enn 1200 x 2 − 400 x − 700 = 0.
Oftere utføres forenkling av formen til en kvadratisk ligning ved å multiplisere eller dele begge sider med et visst tall. For eksempel, ovenfor viste vi en forenklet representasjon av ligningen 1200 x 2 − 400 x − 700 = 0, oppnådd ved å dele begge sider med 100.
En slik transformasjon er mulig når koeffisientene til den kvadratiske ligningen ikke er koprimtall. Da deler vi vanligvis begge sider av ligningen med den største felles deler absolutte verdier dens koeffisienter.
Som et eksempel bruker vi den andregradsligningen 12 x 2 − 42 x + 48 = 0. La oss bestemme GCD for de absolutte verdiene til koeffisientene: GCD (12, 42, 48) = GCD(GCD (12, 42), 48) = GCD (6, 48) = 6. La oss dele begge sider av den opprinnelige andregradsligningen med 6 og få den ekvivalente andregradsligningen 2 x 2 − 7 x + 8 = 0.
Ved å multiplisere begge sider av en andregradsligning, blir du vanligvis kvitt brøkkoeffisienter. I dette tilfellet multipliserer de med det minste felles multiplum av nevnerne til koeffisientene. For eksempel, hvis hver del av andregradsligningen 1 6 x 2 + 2 3 x - 3 = 0 multipliseres med LCM (6, 3, 1) = 6, vil den bli skrevet i mer i enkel form x 2 + 4 x − 18 = 0 .
Til slutt legger vi merke til at vi nesten alltid kvitter oss med minus ved den første koeffisienten til en kvadratisk ligning ved å endre tegnene til hvert ledd i ligningen, som oppnås ved å multiplisere (eller dividere) begge sider med − 1. For eksempel, fra den andregradsligningen − 2 x 2 − 3 x + 7 = 0, kan du gå til dens forenklede versjon 2 x 2 + 3 x − 7 = 0.
Sammenheng mellom røtter og koeffisienter
Formelen for røttene til kvadratiske ligninger, allerede kjent for oss, x = - b ± D 2 · a, uttrykker røttene til ligningen gjennom dens numeriske koeffisienter. Basert på denne formelen har vi mulighet til å spesifisere andre avhengigheter mellom røttene og koeffisientene.
De mest kjente og anvendelige formlene er Vietas teorem:
x 1 + x 2 = - b a og x 2 = c a.
Spesielt for den gitte kvadratiske ligningen er summen av røttene den andre koeffisienten med motsatt tegn, og produktet av røttene er lik frileddet. For eksempel, ved å se på formen til kvadratisk ligning 3 x 2 − 7 x + 22 = 0, er det mulig å umiddelbart bestemme at summen av røttene er 7 3 og produktet av røttene er 22 3.
Du kan også finne en rekke andre sammenhenger mellom røttene og koeffisientene til en kvadratisk ligning. For eksempel kan summen av kvadratene til røttene til en kvadratisk ligning uttrykkes i termer av koeffisienter:
x 1 2 + x 2 2 = (x 1 + x 2) 2 - 2 x 1 x 2 = - b a 2 - 2 c a = b 2 a 2 - 2 c a = b 2 - 2 a c a 2.
Hvis du oppdager en feil i teksten, merk den og trykk Ctrl+Enter
Kopyevskaya landlige ungdomsskole
10 måter å løse kvadratiske ligninger på
Leder: Patrikeeva Galina Anatolyevna,
matematikklærer
landsbyen Kopevo, 2007
1. Historie om utviklingen av andregradsligninger
1.1 Kvadratiske ligninger i det gamle Babylon
1.2 Hvordan Diophantus komponerte og løste andregradsligninger
1.3 Kvadratiske ligninger i India
1.4 Kvadratiske ligninger av al-Khorezmi
1.5 Kvadratiske ligninger i Europa XIII - XVII århundrer
1.6 Om Vietas teorem
2. Metoder for å løse andregradsligninger
Konklusjon
Litteratur
1. Historie om utviklingen av andregradsligninger
1.1 Kvadratiske ligninger i det gamle Babylon
Behovet for å løse ligninger ikke bare av første, men også av andre grad, selv i gamle tider, ble forårsaket av behovet for å løse problemer knyttet til å finne arealer av tomter og med utgravningsarbeid av militær karakter, også som med utviklingen av astronomi og matematikk selv. Kvadratiske ligninger kunne løses rundt 2000 f.Kr. e. babylonere.
Ved å bruke moderne algebraisk notasjon kan vi si at i deres kileskrifttekster er det, i tillegg til ufullstendige, slike for eksempel komplette kvadratiske ligninger:
X 2 + X = ¾; X 2 - X = 14,5
Regelen for å løse disse ligningene, som er angitt i de babylonske tekstene, er i hovedsak sammenfallende med den moderne, men det er ikke kjent hvordan babylonerne kom frem til denne regelen. Nesten alle kileskriftstekster som er funnet så langt gir kun problemer med løsninger lagt opp i form av oppskrifter, uten indikasjon på hvordan de ble funnet.
På tross av høy level utvikling av algebra i Babylon, mangler kileskrifttekstene konseptet med et negativt tall og generelle metoder for å løse andregradsligninger.
1.2 Hvordan Diophantus komponerte og løste andregradsligninger.
Diophantus' Aritmetikk inneholder ikke en systematisk presentasjon av algebra, men den inneholder en systematisk rekke problemer, ledsaget av forklaringer og løst ved å konstruere ligninger av ulike grader.
Når du komponerer ligninger, velger Diophantus dyktig ukjente for å forenkle løsningen.
Her er for eksempel en av oppgavene hans.
Oppgave 11."Finn to tall, vel vitende om at summen deres er 20 og produktet deres er 96"
Diophantus grunner på følgende måte: fra betingelsene for problemet følger det at de nødvendige tallene ikke er like, siden hvis de var like, ville deres produkt ikke være lik 96, men 100. Dermed vil en av dem være mer enn halvparten av summen deres. , dvs. 10 + x, den andre er mindre, dvs. 10-tallet. Forskjellen mellom dem 2x .
Derav ligningen:
(10 + x)(10 - x) = 96
100 - x 2 = 96
x 2 - 4 = 0 (1)
Herfra x = 2. Ett av de nødvendige tallene er lik 12 , annet 8 . Løsning x = -2 for Diophantus eksisterer ikke, siden gresk matematikk bare kjente positive tall.
Hvis vi løser dette problemet ved å velge et av de nødvendige tallene som det ukjente, vil vi komme til en løsning på ligningen
y(20 - y) = 96,
y 2 - 20y + 96 = 0. (2)
Det er klart at ved å velge halvforskjellen til de nødvendige tallene som det ukjente, forenkler Diophantus løsningen; han klarer å redusere problemet til å løse en ufullstendig andregradsligning (1).
1.3 Kvadratiske ligninger i India
Problemer med kvadratiske ligninger finnes allerede i den astronomiske avhandlingen "Aryabhattiam", kompilert i 499 av den indiske matematikeren og astronomen Aryabhatta. En annen indisk vitenskapsmann, Brahmagupta (7. århundre), skisserte generell regel løsninger av kvadratiske ligninger redusert til en enkelt kanonisk form:
ah 2+ b x = c, a > 0. (1)
I ligning (1), koeffisientene, unntatt EN, kan også være negativ. Brahmaguptas styre er i hovedsak det samme som vårt.
I Det gamle India Offentlige konkurranser om å løse vanskelige problemer var vanlig. En av de gamle indiske bøkene sier følgende om slike konkurranser: «Som solen formørker stjernene med sin glans, så lærd mann overskygge en annens herlighet i populære forsamlinger ved å foreslå og løse algebraiske problemer.» Problemer ble ofte presentert i poetisk form.
Dette er et av problemene til den berømte indiske matematikeren på 1100-tallet. Bhaskars.
Oppgave 13.
"En flokk med sprø aper og tolv langs vinrankene ...
Etter å ha spist hadde myndighetene det gøy. De begynte å hoppe, henge...
Det er dem på torget, del åtte. Hvor mange aper var det?
Jeg koste meg i lysningen. Fortell meg, i denne pakken?
Bhaskaras løsning indikerer at han visste at røttene til kvadratiske ligninger er toverdier (fig. 3).
Ligningen som tilsvarer oppgave 13 er:
( x /8) 2 + 12 = x
Bhaskara skriver under dekke:
x 2 - 64x = -768
og for å fullføre venstre side av denne ligningen til kvadrat, legger du til begge sider 32 2 , så får du:
x 2 - 64x + 32 2 = -768 + 1024,
(x - 32) 2 = 256,
x - 32 = ± 16,
x 1 = 16, x 2 = 48.
1.4 Kvadratiske ligninger i al - Khorezmi
I den algebraiske avhandlingen til al-Khorezmi er det gitt en klassifisering av lineære og kvadratiske ligninger. Forfatteren teller 6 typer ligninger, og uttrykker dem som følger:
1) «Kvadrater er lik røtter», dvs. akse 2 + c = b X.
2) «Kvadrater er lik tall», dvs. øks 2 = c.
3) «Røttene er lik tallet», dvs. ah = s.
4) «Kvadrater og tall er lik røtter», dvs. akse 2 + c = b X.
5) «Kvadrater og røtter er lik tall», dvs. ah 2+ bx = s.
6) «Røtter og tall er lik kvadrater», dvs. bx + c = akse 2.
For al-Khorezmi, som unngikk bruken av negative tall, er vilkårene for hver av disse ligningene addisjoner og ikke subtraherbare. I dette tilfellet er det åpenbart ikke tatt hensyn til ligninger som ikke har positive løsninger. Forfatteren angir metoder for å løse disse ligningene ved å bruke teknikkene til al-jabr og al-muqabala. Hans avgjørelser er selvsagt ikke helt sammenfallende med våre. For ikke å nevne at det er rent retorisk, bør det for eksempel bemerkes at når man løser en ufullstendig andregradsligning av den første typen
al-Khorezmi, som alle matematikere før 1600-tallet, tar ikke hensyn til nullløsningen, sannsynligvis fordi praktiske problemer det spiller ingen rolle. Når du løser komplette kvadratiske ligninger, angir al-Khorezmi reglene for å løse dem ved å bruke spesielle numeriske eksempler, og deretter geometriske bevis.
Oppgave 14.«Kvadraten og tallet 21 er lik 10 røtter. Finn roten" (antyder roten av ligningen x 2 + 21 = 10x).
Forfatterens løsning er omtrent slik: del antall røtter i to, du får 5, gang 5 med seg selv, trekk 21 fra produktet, det som gjenstår er 4. Ta roten fra 4, du får 2. Trekk fra 2 fra 5 , får du 3, dette vil være ønsket rot. Eller legg til 2 til 5, som gir 7, dette er også en rot.
Avhandlingen om al-Khorezmi er den første boken som har kommet ned til oss, som systematisk setter opp klassifiseringen av kvadratiske ligninger og gir formler for løsningen deres.
1.5 Kvadratiske ligninger i Europa XIII - XVII bb
Formler for å løse kvadratiske ligninger på linje med al-Khwarizmi i Europa ble først satt frem i Abacus-boken, skrevet i 1202 av den italienske matematikeren Leonardo Fibonacci. Dette omfangsrike arbeidet, som gjenspeiler påvirkningen av matematikk, både islamske land og Antikkens Hellas, kjennetegnes ved både fullstendighet og klarhet i presentasjonen. Forfatteren utviklet uavhengig noen nye algebraiske eksempler løse problemer og var den første i Europa som innførte negative tall. Boken hans bidro til spredningen av algebraisk kunnskap ikke bare i Italia, men også i Tyskland, Frankrike og andre europeiske land. Mange problemer fra Abacus-boken ble brukt i nesten alle europeiske lærebøker på 1500- og 1600-tallet. og delvis XVIII.
Den generelle regelen for å løse kvadratiske ligninger redusert til en enkelt kanonisk form:
x 2 + bx = c,
for alle mulige kombinasjoner av koeffisienttegn b , Med ble formulert i Europa først i 1544 av M. Stiefel.
Avledningen av formelen for å løse en kvadratisk ligning i generell form er tilgjengelig fra Viète, men Viète gjenkjente bare positive røtter. Italienske matematikere Tartaglia, Cardano, Bombelli var blant de første på 1500-tallet. I tillegg til positive, tas også negative røtter i betraktning. Først på 1600-tallet. Takket være arbeidet til Girard, Descartes, Newton og andre vitenskapsmenns måte løse andregradsligninger tar en moderne form.
1.6 Om Vietas teorem
Teoremet som uttrykker forholdet mellom koeffisientene til en kvadratisk ligning og dens røtter, oppkalt etter Vieta, ble formulert av ham for første gang i 1591 som følger: "Hvis B + D, ganget med EN - EN 2 , er lik BD, Det EN er lik I og likeverdig D ».
For å forstå Vieta, bør vi huske det EN, som enhver vokalbokstav, betydde det ukjente (vår X), vokaler I, D- koeffisienter for det ukjente. På språket til moderne algebra betyr Vieta-formuleringen ovenfor: hvis det finnes
(et + b )x - x 2 = ab ,
x 2 - (a + b )x + a b = 0,
x 1 = a, x 2 = b .
Ved å uttrykke forholdet mellom røttene og koeffisientene til ligninger med generelle formler skrevet ved hjelp av symboler, etablerte Viète ensartethet i metodene for å løse ligninger. Men symbolikken til Viet er fortsatt langt fra moderne utseende. Han gjenkjente ikke negative tall, og derfor vurderte han, når han løste ligninger, bare tilfeller der alle røttene var positive.
2. Metoder for å løse andregradsligninger
Kvadratiske ligninger er grunnlaget som det majestetiske byggverket til algebra hviler på. Kvadratiske ligninger er mye brukt for å løse trigonometriske, eksponentielle, logaritmiske, irrasjonelle og transcendentale ligninger og ulikheter. Vi vet alle hvordan vi løser andregradsligninger fra skolen (8. klasse) til eksamen.
Kvadratisk ligning - lett å løse! *Heretter referert til som "KU". Venner, det ser ut til at det ikke kan være noe enklere i matematikk enn å løse en slik ligning. Men noe fortalte meg at mange har problemer med ham. Jeg bestemte meg for å se hvor mange on-demand-visninger Yandex gir ut per måned. Her er hva som skjedde, se:

Hva betyr det? Dette betyr at rundt 70 000 personer per måned søker etter denne informasjonen, hva har denne sommeren med det å gjøre, og hva som vil skje blant skoleår— det blir dobbelt så mange forespørsler. Dette er ikke overraskende, fordi de gutta og jentene som ble uteksaminert fra skolen for lenge siden og forbereder seg til Unified State Exam, leter etter denne informasjonen, og skolebarn prøver også å friske opp hukommelsen.
Til tross for at det er mange sider som forteller deg hvordan du løser denne ligningen, bestemte jeg meg for å også bidra og publisere materialet. For det første vil jeg at besøkende skal komme til nettstedet mitt basert på denne forespørselen; for det andre, i andre artikler, når emnet "KU" kommer opp, vil jeg gi en lenke til denne artikkelen; for det tredje vil jeg fortelle deg litt mer om løsningen hans enn det som vanligvis står på andre nettsteder. La oss komme i gang! Innholdet i artikkelen:
En kvadratisk ligning er en ligning av formen:

hvor koeffisientene a,bog c er vilkårlige tall, med a≠0.
I skolekurset er materialet gitt i følgende form - ligningene er delt inn i tre klasser:
1. De har to røtter.
2. *Ha bare én rot.
3. De har ingen røtter. Det er spesielt verdt å merke seg her at de ikke har ekte røtter
Hvordan beregnes røtter? Bare!
Vi beregner diskriminanten. Under dette "forferdelige" ordet ligger en veldig enkel formel:
![]()
Rotformlene har neste visning:

*Du må kunne disse formlene utenat.
Du kan umiddelbart skrive ned og løse:
Eksempel:

1. Hvis D > 0, så har ligningen to røtter.
2. Hvis D = 0, så har ligningen én rot.
3. Hvis D< 0, то уравнение не имеет действительных корней.
La oss se på ligningen:

I denne forbindelse, når diskriminanten er lik null, sier skolekurset at en rot oppnås, her er den lik ni. Alt er riktig, det er slik, men...
Denne ideen er noe feil. Faktisk er det to røtter. Ja, ja, ikke bli overrasket, du får to like røtter, og for å være matematisk presis, så bør svaret skrive to røtter:
x 1 = 3 x 2 = 3
Men det er så - liten retrett. På skolen kan du skrive det ned og si at det er én rot.
Nå neste eksempel:

Som vi vet kan ikke roten av et negativt tall tas, så det er ingen løsning i dette tilfellet.
Det er hele beslutningsprosessen.
Kvadratisk funksjon.
Dette viser hvordan løsningen ser ut geometrisk. Dette er ekstremt viktig å forstå (i fremtiden, i en av artiklene vil vi analysere i detalj løsningen på den kvadratiske ulikheten).
Dette er en funksjon av skjemaet:

hvor x og y er variabler
a, b, c – gitte tall, med a ≠ 0
Grafen er en parabel:

Det vil si at det viser seg at ved å løse en andregradsligning med "y" lik null, finner vi skjæringspunktene til parabelen med x-aksen. Det kan være to av disse punktene (diskriminanten er positiv), ett (diskriminanten er null) og ingen (diskriminanten er negativ). Detaljer om den kvadratiske funksjonen Du kan se artikkel av Inna Feldman.
La oss se på eksempler:
Eksempel 1: Løs 2x 2 +8 x–192=0
a=2 b=8 c= –192
D=b 2 –4ac = 8 2 –4∙2∙(–192) = 64+1536 = 1600

Svar: x 1 = 8 x 2 = –12
*Det var mulig å umiddelbart dele venstre og høyre side av ligningen med 2, det vil si forenkle den. Beregningene blir lettere.
Eksempel 2: Bestemme seg for x 2–22 x+121 = 0
a=1 b=–22 c=121
D = b 2 –4ac =(–22) 2 –4∙1∙121 = 484–484 = 0

Vi fant at x 1 = 11 og x 2 = 11
Det er lov å skrive x = 11 i svaret.
Svar: x = 11
Eksempel 3: Bestemme seg for x 2 –8x+72 = 0
a=1 b= –8 c=72
D = b 2 –4ac =(–8) 2 –4∙1∙72 = 64–288 = –224
Diskriminanten er negativ, det er ingen løsning i reelle tall.
Svar: ingen løsning
Diskriminanten er negativ. Det finnes en løsning!
Her vil vi snakke om å løse ligningen i tilfellet når en negativ diskriminant oppnås. Kan du noe om komplekse tall? Jeg vil ikke gå i detalj her om hvorfor og hvor de oppsto og hva deres spesifikke rolle og nødvendighet i matematikk er dette er et tema for en stor egen artikkel.
Konseptet med et komplekst tall.
Litt teori.
Et komplekst tall z er et tall av formen
z = a + bi
der a og b er reelle tall, er i den såkalte imaginære enheten.
a+bi – dette er et ENKELT NUMMER, ikke et tillegg.
Den imaginære enheten er lik roten av minus én:

Tenk nå på ligningen:

Vi får to konjugerte røtter.
Ufullstendig andregradsligning.
La oss vurdere spesielle tilfeller, dette er når koeffisienten "b" eller "c" er lik null (eller begge er lik null). De kan løses enkelt uten diskriminering.
Tilfelle 1. Koeffisient b = 0.
Ligningen blir:

La oss transformere:
Eksempel:
4x 2 –16 = 0 => 4x 2 =16 => x 2 = 4 => x 1 = 2 x 2 = –2
Tilfelle 2. Koeffisient c = 0.
Ligningen blir:

La oss transformere og faktorisere:

*Produktet er lik null når minst én av faktorene er lik null.
Eksempel:
9x 2 –45x = 0 => 9x (x–5) =0 => x = 0 eller x–5 =0
x 1 = 0 x 2 = 5
Tilfelle 3. Koeffisientene b = 0 og c = 0.

Her er det klart at løsningen på ligningen alltid vil være x = 0.
Nyttige egenskaper og mønstre av koeffisienter.
Det er egenskaper som lar deg løse ligninger med store koeffisienter.
ENx 2 + bx+ c=0 likestilling holder
en + b+ c = 0, At
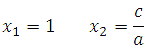
- hvis for koeffisientene til ligningen ENx 2 + bx+ c=0 likestilling holder
en+ c =b, At
![]()
Disse egenskapene hjelper til med å løse en bestemt type ligning.
Eksempel 1: 5001 x 2 –4995 x – 6=0
Summen av oddsen er 5001+( – 4995)+(– 6) = 0, som betyr

Eksempel 2: 2501 x 2 +2507 x+6=0
Likestilling holder en+ c =b, Midler

Regulariteter av koeffisienter.
1. Hvis i ligningen ax 2 + bx + c = 0 er koeffisienten "b" lik (a 2 +1), og koeffisienten "c" er numerisk lik koeffisienten "a", så er røttene like

ax 2 + (a 2 +1)∙x+ a= 0 = > x 1 = –a x 2 = –1/a.
Eksempel. Tenk på ligningen 6x 2 + 37x + 6 = 0.
x 1 = –6 x 2 = –1/6.
2. Hvis i ligningen ax 2 – bx + c = 0 er koeffisienten "b" lik (a 2 +1), og koeffisienten "c" er numerisk lik koeffisienten "a", så er røttene like

ax 2 – (a 2 +1)∙x+ a= 0 = > x 1 = a x 2 = 1/a.
Eksempel. Tenk på ligningen 15x 2 –226x +15 = 0.
x 1 = 15 x 2 = 1/15.
3. Hvis i lign. ax 2 + bx – c = 0 koeffisient "b" er lik (a 2 – 1), og koeffisient "c" er numerisk lik koeffisienten "a", da er røttene like

ax 2 + (a 2 –1)∙x – a= 0 = > x 1 = – a x 2 = 1/a.
Eksempel. Tenk på ligningen 17x 2 +288x – 17 = 0.
x 1 = – 17 x 2 = 1/17.
4. Hvis i ligningen ax 2 – bx – c = 0 er koeffisienten “b” lik (a 2 – 1), og koeffisienten c er numerisk lik koeffisienten “a”, så er røttene like

ax 2 – (a 2 –1)∙x – a= 0 = > x 1 = a x 2 = – 1/a.
Eksempel. Tenk på ligningen 10x 2 – 99x –10 = 0.
x 1 = 10 x 2 = – 1/10
Vietas teorem.
Vietas teorem er oppkalt etter den berømte franske matematikeren Francois Vieta. Ved å bruke Vietas teorem kan vi uttrykke summen og produktet av røttene til en vilkårlig KU i form av koeffisientene.
45 = 1∙45 45 = 3∙15 45 = 5∙9.
Totalt gir tallet 14 kun 5 og 9. Dette er røtter. Med en viss ferdighet, ved å bruke det presenterte teoremet, kan du løse mange andregradsligninger muntlig umiddelbart.
Vietas teorem, i tillegg. praktisk i det etter å ha løst den andregradsligningen på vanlig måte(gjennom diskriminanten) kan de resulterende røttene kontrolleres. Jeg anbefaler å gjøre dette alltid.
TRANSPORTMETODE
Med denne metoden multipliseres koeffisienten "a" med frileddet, som om den ble "kastet" til den, og det er derfor den kalles "overføringsmetode". Denne metoden brukes når røttene til ligningen lett kan finnes ved å bruke Vietas teorem og, viktigst av alt, når diskriminanten er et eksakt kvadrat.
Hvis EN± b+c≠ 0, så brukes overføringsteknikken, for eksempel:
2X 2 – 11x+ 5 = 0 (1) => X 2 – 11x+ 10 = 0 (2)
Ved å bruke Vietas teorem i ligning (2), er det lett å bestemme at x 1 = 10 x 2 = 1
De resulterende røttene til ligningen må deles på 2 (siden de to ble "kastet" fra x 2), får vi
x 1 = 5 x 2 = 0,5.
Hva er begrunnelsen? Se hva som skjer.
Diskriminantene til ligningene (1) og (2) er like:
Hvis du ser på røttene til ligningene, får du bare forskjellige nevnere, og resultatet avhenger nøyaktig av koeffisienten til x 2:

Den andre (modifiserte) har røtter som er 2 ganger større.
Derfor deler vi resultatet på 2.
*Hvis vi ruller de tre på nytt, deler vi resultatet med 3 osv.
Svar: x 1 = 5 x 2 = 0,5
Sq. ur-ie og Unified State Examination.
Jeg skal fortelle deg kort om viktigheten - DU MÅ KUNNE AVGJØRE raskt og uten å tenke, du må kunne formlene for røtter og diskriminanter utenat. Mange av problemene inkludert i Unified State Examination-oppgavene kommer ned til å løse en kvadratisk ligning (inkludert geometriske).
Noe verdt å merke seg!
1. Formen for å skrive en ligning kan være "implisitt". For eksempel er følgende oppføring mulig:
15+ 9x 2 - 45x = 0 eller 15x+42+9x 2 - 45x=0 eller 15 -5x+10x 2 = 0.
Du må bringe det til et standardskjema (for ikke å bli forvirret når du løser).
2. Husk at x er en ukjent størrelse og den kan betegnes med en hvilken som helst annen bokstav - t, q, p, h og andre.
Noen problemer i matematikk krever evnen til å beregne verdien av kvadratroten. Slike problemer inkluderer å løse andreordens ligninger. I denne artikkelen vil vi presentere effektiv metode beregninger kvadratrøtter og bruk det når du arbeider med formler for røttene til en andregradsligning.
Hva er en kvadratrot?
I matematikk tilsvarer dette konseptet symbolet √. Historiske data sier at det først ble brukt rundt første halvdel av 1500-tallet i Tyskland (det første tyske verket om algebra av Christoph Rudolf). Forskere tror at det angitte symbolet er en transformert latinsk bokstav r (radix betyr "rot" på latin).
Roten til et hvilket som helst tall er lik verdien hvis kvadrat tilsvarer det radikale uttrykket. På matematikkspråket vil denne definisjonen se slik ut: √x = y, hvis y 2 = x.
Roten av positivt tall(x > 0) er også et positivt tall (y > 0), men hvis du tar roten av et negativt tall (x< 0), то его результатом уже будет комплексное число, включающее мнимую единицу i.
Her er to enkle eksempler:
√9 = 3, siden 3 2 = 9; √(-9) = 3i, siden i 2 = -1.
Herons iterative formel for å finne verdiene til kvadratrøtter
Eksemplene ovenfor er veldig enkle, og det er ikke vanskelig å beregne røttene i dem. Vanskeligheter begynner å dukke opp når du finner rotverdier for enhver verdi som ikke kan representeres som en kvadrat naturlig tall, for eksempel √10, √11, √12, √13, for ikke å nevne det faktum at det i praksis er nødvendig å finne røtter for ikke-heltall: for eksempel √(12,15), √(8,5) og så videre.

I alle de ovennevnte tilfellene bør du bruke spesiell metode kvadratrotberegninger. For tiden er flere slike metoder kjent: for eksempel utvidelse av Taylor-serien, kolonnedeling og noen andre. Av alle de kjente metodene er kanskje den enkleste og mest effektive bruken av Herons iterative formel, som også er kjent som den babylonske metoden for å bestemme kvadratrøtter (det er bevis på at de gamle babylonerne brukte den i sine praktiske beregninger).
La det være nødvendig å bestemme verdien av √x. Finne formel kvadratrot har følgende form:
a n+1 = 1/2(a n +x/a n), hvor lim n->∞ (a n) => x.
La oss dechiffrere denne matematiske notasjonen. For å beregne √x, bør du ta et visst tall a 0 (det kan være vilkårlig, men for raskt å få resultatet, bør du velge det slik at (a 0) 2 er så nært x som mulig. Deretter erstatter du det i angitt formel for å beregne kvadratroten og få en ny tallet en 1, som allerede vil være nærmere den ønskede verdien Etter dette, er det nødvendig å erstatte en 1 i uttrykket og få en 2. Denne prosedyren bør gjentas til den nødvendige nøyaktigheten oppnås.
Et eksempel på bruk av Herons iterative formel
Algoritmen beskrevet ovenfor for å få kvadratroten av et gitt tall kan høres ganske komplisert og forvirrende ut for mange, men i virkeligheten viser alt seg å være mye enklere, siden denne formelen konvergerer veldig raskt (spesielt hvis et vellykket tall a 0 er valgt) .
La oss gi et enkelt eksempel: du må regne ut √11. La oss velge en 0 = 3, siden 3 2 = 9, som er nærmere 11 enn 4 2 = 16. Ved å sette inn i formelen får vi:
a 1 = 1/2(3 + 11/3) = 3,333333;
a 2 = 1/2(3,33333 + 11/3,33333) = 3,316668;
a 3 = 1/2(3,316668 + 11/3,316668) = 3,31662.
Det er ingen vits i å fortsette beregningene, siden vi fant at en 2 og en 3 begynner å avvike bare på 5. desimal. Dermed var det nok å bruke formelen bare 2 ganger for å beregne √11 med en nøyaktighet på 0,0001.
I dag er kalkulatorer og datamaskiner mye brukt til å beregne røtter, men det er nyttig å huske den merkede formelen for å kunne beregne deres nøyaktige verdi manuelt.
Andre ordens ligninger
Å forstå hva en kvadratrot er og evnen til å beregne den brukes til å løse andregradsligninger. Disse ligningene kalles likheter med en ukjent, generell form som er vist i figuren under.

Her representerer c, b og a noen tall, og a må ikke være lik null, og verdiene til c og b kan være helt vilkårlige, inkludert lik null.
Alle verdier av x som tilfredsstiller likheten angitt i figuren kalles røttene (dette konseptet skal ikke forveksles med kvadratroten √). Siden ligningen som vurderes er av 2. orden (x 2), kan det ikke være mer enn to røtter for den. La oss se videre i artikkelen på hvordan du finner disse røttene.
Finne røttene til en andregradsligning (formel)
Denne metoden for å løse typen likheter som vurderes kalles også den universelle metoden, eller diskriminantmetoden. Den kan brukes til alle andregradsligninger. Formelen for diskriminanten og røttene til den kvadratiske ligningen er som følger:

Den viser at røttene avhenger av verdien av hver av de tre koeffisientene i ligningen. Dessuten skiller beregningen av x 1 seg fra beregningen av x 2 bare ved tegnet foran kvadratroten. Det radikale uttrykket, som er lik b 2 - 4ac, er ikke annet enn diskriminanten av den aktuelle likheten. Diskriminanten i formelen for røttene til en andregradsligning spiller viktig rolle, siden det bestemmer antall og type løsninger. Så hvis den er lik null, vil det bare være én løsning, hvis den er positiv, så har ligningen to reelle røtter, og til slutt fører en negativ diskriminant til to komplekse røtter x 1 og x 2.
Vietas teorem eller noen egenskaper til røttene til andreordens ligninger
På slutten av 1500-tallet var en av grunnleggerne av moderne algebra, en franskmann, som studerte annenordens ligninger, i stand til å få egenskapene til røttene. Matematisk kan de skrives slik:
x 1 + x 2 = -b / a og x 1 * x 2 = c / a.
Begge likhetene kan enkelt oppnås av alle for å gjøre dette, du trenger bare å utføre de riktige matematiske operasjonene med røttene oppnådd gjennom formelen med diskriminanten.

Kombinasjonen av disse to uttrykkene kan med rette kalles den andre formelen for røttene til en kvadratisk ligning, som gjør det mulig å gjette løsningene uten å bruke en diskriminant. Her bør det bemerkes at selv om begge uttrykkene alltid er gyldige, er det praktisk å bruke dem til å løse en ligning bare hvis den kan faktoriseres.
Oppgaven med å konsolidere den ervervede kunnskapen
La oss løse et matematisk problem der vi vil demonstrere alle teknikkene som er diskutert i artikkelen. Betingelsene for problemet er som følger: du må finne to tall der produktet er -13 og summen er 4.

Denne tilstanden minner oss umiddelbart om Vietas teorem ved å bruke formlene for summen av kvadratrøtter og deres produkt, vi skriver:
x 1 + x 2 = -b/a = 4;
x 1 * x 2 = c/a = -13.
Hvis vi antar at a = 1, så er b = -4 og c = -13. Disse koeffisientene lar oss lage en andreordens ligning:
x 2 - 4x - 13 = 0.
La oss bruke formelen med diskriminanten og få følgende røtter:
x 1,2 = (4 ± √D)/2, D = 16 - 4 * 1 * (-13) = 68.
Det vil si at problemet ble redusert til å finne tallet √68. Legg merke til at 68 = 4 * 17, så, ved å bruke kvadratrotegenskapen, får vi: √68 = 2√17.
La oss nå bruke den betraktede kvadratrotformelen: a 0 = 4, så:
a 1 = 1/2(4 + 17/4) = 4,125;
a 2 = 1/2(4,125 + 17/4,125) = 4,1231.
Det er ikke nødvendig å beregne en 3 siden verdiene som ble funnet avviker med bare 0,02. Dermed er √68 = 8,246. Ved å erstatte det med formelen for x 1,2 får vi:
x 1 = (4 + 8,246)/2 = 6,123 og x 2 = (4 - 8,246)/2 = -2,123.
Som vi kan se, er summen av tallene funnet egentlig lik 4, men hvis vi finner produktet deres, vil det være lik -12,999, som tilfredsstiller betingelsene for problemet med en nøyaktighet på 0,001.
