Lesson plan on the topic: Homogeneous trigonometric equations. Systems with nonlinear equations
Nonlinear equations with two unknowns
Definition 1. Let A be some set of pairs of numbers (x; y) . They say that the set A is given numeric function z from two variables x and y , if a rule is specified with the help of which each pair of numbers from set A is associated with a certain number.
Specifying a numerical function z of two variables x and y is often denote So:
Where f (x , y) – any function other than a function
f (x , y) = ax+by+c ,
where a, b, c are given numbers.
Definition 3. Solving equation (2) call a pair of numbers ( x; y) , for which formula (2) is a true equality.
Example 1. Solve the equation
Since the square of any number is non-negative, it follows from formula (4) that the unknowns x and y satisfy the system of equations

the solution to which is a pair of numbers (6; 3).
Answer: (6; 3)
Example 2. Solve the equation
Therefore, the solution to equation (6) is infinite number of pairs of numbers kind
(1 + y ; y) ,
where y is any number.
linear
Definition 4. Solving a system of equations

call a pair of numbers ( x; y) , when substituting them into each of the equations of this system, the correct equality is obtained.
Systems of two equations, one of which is linear, have the form
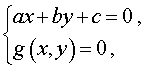
g(x , y)
Example 4. Solve system of equations
Solution . Let us express the unknown y from the first equation of system (7) through the unknown x and substitute the resulting expression into the second equation of the system:


Solving the equation
x 1 = - 1 , x 2 = 9 .
Hence,
y 1 = 8 - x 1 = 9 ,
y 2 = 8 - x 2 = - 1 .


Systems of two equations, one of which is homogeneous
Systems of two equations, one of which is homogeneous, have the form

where a, b, c are given numbers, and g(x , y) – function of two variables x and y.
Example 6. Solve system of equations
Solution . Let's solve the homogeneous equation
3x 2 + 2xy - y 2 = 0 ,
3x 2 + 17xy + 10y 2 = 0 ,
treating it as a quadratic equation with respect to the unknown x:
 .
.
In case x = - 5y, from the second equation of system (11) we obtain the equation
5y 2 = - 20 ,
which has no roots.
In case
from the second equation of system (11) we obtain the equation
 ,
,
whose roots are numbers y 1 = 3 , y 2 = - 3 . Finding for each of these values y the corresponding value x, we obtain two solutions to the system: (- 2 ; 3) , (2 ; - 3) .
Answer: (- 2 ; 3) , (2 ; - 3)
Examples of solving systems of equations of other types
Example 8. Solve a system of equations (MIPT)
Solution . Let us introduce new unknowns u and v, which are expressed through x and y according to the formulas:
In order to rewrite system (12) in terms of new unknowns, we first express the unknowns x and y in terms of u and v. From system (13) it follows that
Let us solve the linear system (14) by eliminating the variable x from the second equation of this system. For this purpose, we perform the following transformations on system (14):
- We will leave the first equation of the system unchanged;
- from the second equation we subtract the first equation and replace the second equation of the system with the resulting difference.
As a result, system (14) is transformed into an equivalent system

from which we find
Using formulas (13) and (15), we rewrite the original system (12) in the form
The first equation of system (16) is linear, so we can express from it the unknown u through the unknown v and substitute this expression into the second equation of the system.
In this article we will look at a method for solving homogeneous trigonometric equations.
Homogeneous trigonometric equations have the same structure as homogeneous equations of any other type. Let me remind you of the method for solving homogeneous equations of the second degree:
Let us consider homogeneous equations of the form
Distinctive features of homogeneous equations:
a) all monomials have the same degree,
b) the free term is zero,
c) the equation contains powers with two different bases.
Homogeneous equations are solved using a similar algorithm.
To solve this type of equation, we divide both sides of the equation by (can be divided by or by)
Attention! When dividing the right and left sides of an equation by an expression containing an unknown, you can lose roots. Therefore, it is necessary to check whether the roots of the expression by which we divide both sides of the equation are the roots of the original equation.
If it is, then we write down this root so that we don’t forget about it later, and then divide the expression by this.
In general, the first thing to do when solving any equation that has a zero on the right side is to try to factor the left side of the equation into any in an accessible way. And then equate each factor to zero. In this case, we will definitely not lose the roots.
So, carefully divide the left side of the equation into the expression term by term. We get:

Let's reduce the numerator and denominator of the second and third fractions:

Let's introduce the replacement:
We get quadratic equation:
![]()
Let's solve the quadratic equation, find the values of , and then return to the original unknown.
When solving homogeneous trigonometric equations, there are several important things to remember:
1. The dummy term can be converted to the square of sine and cosine using the basic trigonometric identity:
2. The sine and cosine of a double argument are monomials of the second degree - the sine of a double argument can be easily converted to the product of sine and cosine, and the cosine of a double argument to the square of sine or cosine:
Let's look at several examples of solving homogeneous trigonometric equations.
1. Let's solve the equation:
This is a classic example of a homogeneous trigonometric equation of the first degree: the degree of each monomial is equal to one, the free term is equal to zero.
Before dividing both sides of the equation by , you need to check that the roots of the equation are not the roots of the original equation. We check: if , then title="sin(x)0">, следовательно их сумма не равна нулю.!}
Let's divide both sides of the equation by .
We get: ![]()
![]() , Where
, Where
![]() , Where
, Where
Answer: ![]() , Where
, Where
2. Let's solve the equation:
This is an example of a homogeneous trigonometric equation of the second degree. We remember that if we can factor the left side of the equation, then it is advisable to do so. In this equation we can put . Let's do this:
![]()

Solution of the first equation: , where
The second equation is a homogeneous trigonometric equation of the first degree. To solve it, divide both sides of the equation by . We get:
![]()
Answer: , where ,
3. Let's solve the equation:
To make this equation “become” homogeneous, we transform it into a product and present the number 3 as the sum of the squares of sine and cosine:
Let's move all the terms to the left, open the brackets and present similar terms. We get:
![]()
Let's factorize the left side and set each factor equal to zero:
![]()
Answer: , where ,
4. Let's solve the equation:
We see what we can take out of the brackets. Let's do this:
Let's equate each factor to zero:

Solution of the first equation:
The second population equation is a classical homogeneous equation of the second degree. The roots of the equation are not the roots of the original equation, so we divide both sides of the equation by:

![]()
Solution of the first equation:
Solution of the second equation.
With this video lesson, students will be able to study the topic of homogeneous trigonometric equations.
Let's give definitions:
1) a homogeneous trigonometric equation of the first degree looks like a sin x + b cos x = 0;
2) a homogeneous trigonometric equation of the second degree looks like a sin 2 x + b sin x cos x + c cos 2 x = 0.
Consider the equation a sin x + b cos x = 0. If a is equal to zero, then the equation will look like b cos x = 0; if b is equal to zero, then the equation will look like a sin x = 0. These are the equations that we called the simplest and were solved earlier in previous topics.
Now consider the option when a and b are not equal to zero. By dividing the parts of the equation by the cosine x, we carry out the transformation. We get a tg x + b = 0, then tg x will be equal to - b/a.
From the above it follows that the equation a sin mx + b cos mx = 0 is homogeneous trigonometric equation I degree. To solve an equation, divide its parts by cos mx.
Let's look at example 1. Solve 7 sin (x/2) - 5 cos (x/2) = 0. First, divide the parts of the equation by cosine (x/2). Knowing that sine divided by cosine is tangent, we get 7 tan (x/2) - 5 = 0. Transforming the expression, we find that the value of tan (x/2) is equal to 5/7. The solution to this equation has the form x = arctan a + πn, in our case x = 2 arctan (5/7) + 2πn.
Consider the equation a sin 2 x + b sin x cos x + c cos 2 x = 0:
1) with a equal to zero, the equation will look like b sin x cos x + c cos 2 x = 0. Transforming, we obtain the expression cos x (b sin x + c cos x) = 0 and proceed to solving two equations. After dividing the parts of the equation by the cosine x, we get b tg x + c = 0, which means tg x = - c/b. Knowing that x = arctan a + πn, then the solution in in this case will be x = arctan (- c/b) + πn.
2) if a is not equal to zero, then by dividing the parts of the equation by the cosine squared, we obtain an equation containing a tangent, which will be quadratic. This equation can be solved by introducing a new variable.
3) when c is equal to zero, the equation will take the form a sin 2 x + b sin x cos x = 0. This equation can be solved if we take the sine of x out of brackets.
1. see if the equation contains a sin 2 x;
2. If the equation contains the term a sin 2 x, then the equation can be solved by dividing both sides by the squared cosine and then introducing a new variable.
3. If the equation does not contain a sin 2 x, then the equation can be solved by taking cosx out of brackets.
Let's consider example 2. Let's take the cosine out of brackets and get two equations. The root of the first equation is x = π/2 + πn. To solve the second equation, we divide the parts of this equation by the cosine x, and by transformation we obtain x = π/3 + πn. Answer: x = π/2 + πn and x = π/3 + πn.
Let's solve example 3, an equation of the form 3 sin 2 2x - 2 sin 2x cos 2x + 3 cos 2 2x = 2 and find its roots, which belong to the segment from - π to π. Because This equation is inhomogeneous, it is necessary to bring it to a homogeneous form. Using the formula sin 2 x + cos 2 x = 1, we get the equation sin 2 2x - 2 sin 2x cos 2x + cos 2 2x = 0. Dividing all parts of the equation by cos 2 x, we get tg 2 2x + 2tg 2x + 1 = 0 . Using the input of a new variable z = tan 2x, we solve the equation whose root is z = 1. Then tan 2x = 1, which implies that x = π/8 + (πn)/2. Because according to the conditions of the problem, you need to find the roots that belong to the segment from - π to π, the solution will have the form - π< x <π. Подставляя найденное значение x в данное выражение и преобразовывая его, получим - 2,25 < n < 1,75. Т.к. n - это целые числа, то решению уравнения удовлетворяют значения n: - 2; - 1; 0; 1. При этих значениях n получим корни решения исходного уравнения: x = (- 7π)/8, x = (- 3π)/8, x =π/8, x = 5π/8.
TEXT DECODING:
Homogeneous trigonometric equations
Today we will look at how “Homogeneous trigonometric equations” are solved. These are equations of a special type.
Let's get acquainted with the definition.
Equation of the form and sin x+bcosx = 0 (and sine x plus be cosine x is equal to zero) is called a homogeneous trigonometric equation of the first degree;
equation of the form and sin 2 x+bsin xcosx+scos 2 x= 0 (and sine square x plus be sine x cosine x plus se cosine square x equals zero) is called a homogeneous trigonometric equation of the second degree.
If a=0, then the equation takes the form bcosx = 0.
If b = 0 , then we get and sin x= 0.
These equations are elementary trigonometric, and we discussed their solution in our previous topics
Let's consider the case when both coefficients are not equal to zero. Let's divide both sides of the equation Asinx+ bcosx = 0 member by member cosx.
We can do this since the cosine of x is non-zero. After all, if cosx = 0 , then the equation Asinx+ bcosx = 0 will take the form Asinx = 0 , A≠ 0, therefore sinx = 0 . Which is impossible, because according to the basic trigonometric identity sin 2 x+cos 2 x=1 .
Dividing both sides of the equation Asinx+ bcosx = 0 member by member cosx, we get: + =0
Let's carry out the transformations:
1. Since = tg x, then =and tg x
2 reduce by cosx, Then
Thus we get the following expression and tg x + b =0.

Let's carry out the transformation:
1.move b to the right side of the expression with the opposite sign
and tg x =- b
2. Let's get rid of the multiplier and dividing both sides of the equation by a
tan x= -.
Conclusion: Equation of the form a sinmx+bcosmx = 0 (and sine em x plus be cosine em x equals zero) is also called a homogeneous trigonometric equation of the first degree. To solve it, divide both sides by cosmx.
EXAMPLE 1. Solve the equation 7 sin - 5 cos = 0 (seven sine x over two minus five cosine x over two equals zero)
Solution. Dividing both sides of the equation term by cos, we get
1. = 7 tan (since the ratio of sine to cosine is a tangent, then seven sine x by two divided by cosine x by two is equal to 7 tan x by two)
2. -5 = -5 (with cos abbreviation)
This way we got the equation
7tg - 5 = 0, Let's transform the expression, move minus five to the right side, changing the sign.
We have reduced the equation to the form tg t = a, where t=, a =. And since this equation has a solution for any value A and these solutions have the form
x = arctan a + πn, then the solution to our equation will have the form:
Arctg + πn, find x
x=2 arctan + 2πn.
Answer: x=2 arctan + 2πn.
Let us move on to the homogeneous trigonometric equation of the second degree
Asin 2 x+b sin x cos x +Withcos 2 x= 0.
Let's consider several cases.
I. If a=0, then the equation takes the form bsinxcosx+scos 2 x= 0.
When solving e Then we use the method of factorization of the equations. We'll take it out cosx beyond the bracket and we get: cosx(bsinx+scosx)= 0 . Where cosx= 0 or
b sin x +Withcos x= 0. And we already know how to solve these equations.

Let's divide both sides of the equation term by cosх, we get
1 (since the ratio of sine to cosine is a tangent).
Thus we get the equation: b tg x+c=0
We have reduced the equation to the form tg t = a, where t= x, a =. And since this equation has a solution for any value A and these solutions have the form
x = arctan a + πn, then the solution to our equation will be:
x = arctan + πn, .
II. If a≠0, then we divide both sides of the equation term by term into cos 2 x.
(Arguing in a similar way, as in the case of a homogeneous trigonometric equation of the first degree, cosine x cannot go to zero).
III. If c=0, then the equation takes the form Asin 2 x+ bsinxcosx= 0. This equation can be solved by factorization method (we take out sinx beyond the bracket).
This means that when solving the equation Asin 2 x+ bsinxcosx+scos 2 x= 0 you can follow the algorithm:
EXAMPLE 2. Solve the equation sinxcosx - cos 2 x= 0 (sine x times cosine x minus root of three times cosine square x equals zero).
Solution. Let's factorize it (put cosx out of brackets). We get
cos x(sin x - cos x)= 0, i.e. cos x=0 or sin x - cos x= 0.
Answer: x =+ πn, x= + πn.
EXAMPLE 3. Solve the equation 3sin 2 2x - 2 sin2xcos2 x +3cos 2 2x= 2 (three sine squared two x minus twice the product of sine two x times cosine two x plus three cosine squared two x) and find its roots belonging to the interval (- π;
Solution. This equation is not homogeneous, so let's make some transformations. We replace the number 2 contained on the right side of the equation with the product 2 1
Since by the main trigonometric identity sin 2 x + cos 2 x =1, then
2 ∙ 1= 2 ∙ (sin 2 x + cos 2 x) = opening the brackets we get: 2 sin 2 x + 2 cos 2 x.
2 ∙ 1= 2 ∙ (sin 2 x + cos 2 x) =2 sin 2 x + 2 cos 2 x
This means that the equation 3sin 2 2x - 2 sin2xcos2 x +3cos 2 2x= 2 will take the form:
3sin 2 2x - 2 sin 2x cos2 x +3cos 2 2x = 2 sin 2 x + 2 cos 2 x.
3sin 2 2x - 2 sin 2x cos2 x +3cos 2 2x - 2 sin 2 x - 2 cos 2 x=0,
sin 2 2x - 2 sin 2x cos2 x +cos 2 2x =0.
We obtained a homogeneous trigonometric equation of the second degree. Let's apply the method of term-by-term division by cos 2 2x:
tg 2 2x - 2tg 2x + 1 = 0.
Let's introduce a new variable z= tan2x.
We have z 2 - 2 z + 1 = 0. This is a quadratic equation. Noticing the abbreviated multiplication formula on the left side - the square of the difference (), we obtain (z - 1) 2 = 0, i.e. z = 1. Let's return to the reverse substitution:

We have reduced the equation to the form tg t = a, where t= 2x, a =1. And since this equation has a solution for any value A and these solutions have the form
x = arctan x a + πn, then the solution to our equation will be:
2х= arctan1 + πn,
x = + , (x is equal to the sum of pi times eight and pi en times two).
All we have to do is find values of x that are contained in the interval
(- π; π), i.e. satisfy the double inequality - π x π. Because
x= +, then - π + π. Divide all parts of this inequality by π and multiply by 8, we get
move one to the right and to the left, changing the sign to minus one
divide by four we get,
For convenience, we separate the whole parts in fractions
- This inequality is satisfied by the following integer n: -2, -1, 0, 1 Today we will study homogeneous trigonometric equations. First, let's look at the terminology: what is a homogeneous trigonometric equation. It has the following characteristics: And if everything is clear with the first point, then it’s worth talking about the second in more detail. What does it mean to have the same degree of terms? Let's look at the first problem: 3cosx+5sinx=0 3\cos x+5\sin x=0 The first term in this equation is 3cosx 3\cos x. Please note that there is only one trigonometric function here - cosx\cos x - and no other trigonometric functions are present here, so the degree of this term is 1. The same with the second - 5sinx 5\sin x - only sine is present here, i.e. the degree of this term is also equal to one. So, we have before us an identity consisting of two elements, each of which contains a trigonometric function, and only one. This is a first degree equation. Let's move on to the second expression: 4sin2
x+sin2x−3=0 4((\sin )^(2))x+\sin 2x-3=0 The first member of this construction is 4sin2
x 4((\sin )^(2))x. Now we can write the following solution: sin2
x=sinx⋅sinx ((\sin )^(2))x=\sin x\cdot \sin x In other words, the first term contains two trigonometric functions, i.e. its degree is two. Let's deal with the second element - sin2x\sin 2x. Let's remember this formula - the double angle formula: sin2x=2sinx⋅cosx \sin 2x=2\sin x\cdot \cos x And again, in the resulting formula we have two trigonometric functions - sine and cosine. Thus, the power value of this term of the construction is also equal to two. Let's move on to the third element - 3. We remember from the high school mathematics course that any number can be multiplied by 1, so we write it down: ˜
3=3⋅1
And the unit can be written using the basic trigonometric identity in the following form: 1=sin2
x⋅ cos2
x 1=((\sin )^(2))x\cdot ((\cos )^(2))x Therefore, we can rewrite 3 as follows: 3=3(sin2
x⋅ cos2
x)=3sin2
x+3 cos2
x 3=3\left(((\sin )^(2))x\cdot ((\cos )^(2))x \right)=3((\sin )^(2))x+3(( \cos )^(2))x Thus, our term 3 is divided into two elements, each of which is homogeneous and has a second degree. The sine in the first term occurs twice, the cosine in the second also occurs twice. Thus, 3 can also be represented as a term with a power exponent of two. Same thing with the third expression: sin3
x+ sin2
xcosx=2 cos3
x Let's see. The first term is sin3
x((\sin )^(3))x is a trigonometric function of the third degree. Second element - sin2
xcosx((\sin )^(2))x\cos x. sin2
((\sin )^(2)) is a link with power value two multiplied by cosx\cos x is the first term. In total, the third term also has a power value of three. Finally, on the right there is another link - 2cos3
x 2((\cos )^(3))x is an element of the third degree. Thus, we have before us a homogeneous trigonometric equation of the third degree. We have three identities of different degrees written down. Pay attention again to the second expression. In the original record, one of the members has an argument 2x 2x. We are forced to get rid of this argument by transforming it using the double angle sine formula, because all functions included in our identity must necessarily have the same argument. And this is a requirement for homogeneous trigonometric equations. We've sorted out the terms, let's move on to the solution. Regardless of the power exponent, solving equalities of this type is always performed in two steps: 1) prove that cosx≠0 \cos x\ne 0. To do this, it is enough to recall the formula of the main trigonometric identity (sin2
x⋅ cos2
x=1)\left(((\sin )^(2))x\cdot ((\cos )^(2))x=1 \right) and substitute into this formula cosx=0\cos x=0. We will get the following expression: sin2
x=1sinx=±1 \begin(align)& ((\sin )^(2))x=1 \\& \sin x=\pm 1 \\\end(align) Substituting the obtained values, i.e. instead of cosx\cos x is zero, and instead sinx\sin x — 1 or -1, into the original expression, we will get an incorrect numerical equality. This is the justification that cosx≠0 2) the second step logically follows from the first. Since cosx≠0 \cos x\ne 0, we divide both of our sides of the structure by cosn x((\cos )^(n))x, where n n is the power exponent itself of a homogeneous trigonometric equation. What does this give us: \[\begin(array)(·(35)(l)) sinxcosx=tgxcosxcosx=1
\begin(align)& \frac(\sin x)(\cos x)=tgx \\& \frac(\cos x)(\cos x)=1 \\\end(align) \\() \\ \end(array)\] Thanks to this, our cumbersome initial construction is reduced to the equation n n-degree with respect to tangent, the solution of which can be easily written using a change of variable. That's the whole algorithm. Let's see how it works in practice. 3cosx+5sinx=0 3\cos x+5\sin x=0 We have already found out that this is a homogeneous trigonometric equation with a power exponent equal to one. Therefore, first of all, let’s find out that cosx≠0\cos x\ne 0. Suppose the opposite, that cosx=0→sinx=±1 \cos x=0\to \sin x=\pm 1. We substitute the resulting value into our expression, we get: 3⋅0+5⋅(±1) =0±5=0 \begin(align)& 3\cdot 0+5\cdot \left(\pm 1 \right)=0 \\& \pm 5=0 \\\end(align) Based on this we can say that cosx≠0\cos x\ne 0. Divide our equation by cosx\cos x because our entire expression has a power value of one. We get: 3(cosxcosx)
+5(sinxcosx)
=0
3+5tgx=0tgx=− 3
5
\begin(align)& 3\left(\frac(\cos x)(\cos x) \right)+5\left(\frac(\sin x)(\cos x) \right)=0 \\& 3+5tgx=0 \\& tgx=-\frac(3)(5) \\\end(align) This is not a table value, so the answer will include arctgx arctgx: x=arctg (−3
5
)
+ π n,n∈Z x=arctg\left(-\frac(3)(5) \right)+\text( )\!\!\pi\!\!\text( )n,n\in Z Since arctg arctg arctg is an odd function, we can take the “minus” out of the argument and put it in front of arctg. We get the final answer: x=−arctg 3
5
+ π n,n∈Z x=-arctg\frac(3)(5)+\text( )\!\!\pi\!\!\text( )n,n\in Z 4sin2
x+sin2x−3=0 4((\sin )^(2))x+\sin 2x-3=0 As you remember, before you start solving it, you need to perform some transformations. We carry out the transformations: 4sin2
x+2sinxcosx−3 (sin2
x+ cos2
x)=0
4sin2
x+2sinxcosx−3 sin2
x−3 cos2
x=0sin2
x+2sinxcosx−3 cos2
x=0 \begin(align)& 4((\sin )^(2))x+2\sin x\cos x-3\left(((\sin )^(2))x+((\cos )^(2 ))x \right)=0 \\& 4((\sin )^(2))x+2\sin x\cos x-3((\sin )^(2))x-3((\cos )^(2))x=0 \\& ((\sin )^(2))x+2\sin x\cos x-3((\cos )^(2))x=0 \\\end (align) We received a structure consisting of three elements. In the first term we see sin2
((\sin )^(2)), i.e. its power value is two. In the second term we see sinx\sin x and cosx\cos x - again there are two functions, they are multiplied, so the total degree is again two. In the third link we see cos2
x((\cos )^(2))x - similar to the first value. Let's prove that cosx=0\cos x=0 is not a solution to this construction. To do this, let's assume the opposite: \[\begin(array)(·(35)(l)) \cos x=0 \\\sin x=\pm 1 \\1+2\cdot \left(\pm 1 \right)\cdot 0-3\cdot 0=0 \\1+0-0=0 \ \1=0 \\\end(array)\] We have proven that cosx=0\cos x=0 cannot be a solution. Let's move on to the second step - divide our entire expression by cos2
x((\cos )^(2))x. Why squared? Because the power exponent of this homogeneous equation is equal to two: sin2
xcos2
x+2sinxcosxcos2
x−3=0
t g2
x+2tgx−3=0 \begin(align)& \frac(((\sin )^(2))x)(((\cos )^(2))x)+2\frac(\sin x\cos x)(((\ cos )^(2))x)-3=0 \\& t((g)^(2))x+2tgx-3=0 \\\end(align) Is it possible to solve this expression using a discriminant? Of course you can. But I propose to recall the theorem converse to Vieta’s theorem, and we get that we can represent this polynomial in the form of two simple polynomials, namely: (tgx+3) (tgx−1) =0tgx=−3→x=−arctg3+ π n,n∈Ztgx=1→x= π
4
+ π k,k∈Z \begin(align)& \left(tgx+3 \right)\left(tgx-1 \right)=0 \\& tgx=-3\to x=-arctg3+\text( )\!\!\pi\ !\!\text( )n,n\in Z \\& tgx=1\to x=\frac(\text( )\!\!\pi\!\!\text( ))(4)+\ text( )\!\!\pi\!\!\text( )k,k\in Z \\\end(align) Many students ask whether it is worth writing separate coefficients for each group of solutions to identities or not bothering and writing the same ones everywhere. Personally, I believe that it is better and more reliable to use different letters, so that if you enter a serious technical university with additional tests in mathematics, the examiners will not find fault with the answer. sin3
x+ sin2
xcosx=2 cos3
x ((\sin )^(3))x+((\sin )^(2))x\cos x=2((\cos )^(3))x We already know that this is a homogeneous trigonometric equation of the third degree, no special formulas are needed, and all that is required of us is to move the term 2cos3
x 2((\cos )^(3))x to the left. Let's rewrite: sin3
x+ sin2
xcosx−2 cos3
x=0 ((\sin )^(3))x+((\sin )^(2))x\cos x-2((\cos )^(3))x=0 We see that each element contains three trigonometric functions, so this equation has a power value of three. Let's solve it. First of all, we need to prove that cosx=0\cos x=0 is not a root: \[\begin(array)(·(35)(l)) \cos x=0 \\\sin x=\pm 1 \\\end(array)\] Let's substitute these numbers into our original construction: (±1)3
+1⋅0−2⋅0=0
±1+0−0=0±1=0 \begin(align)& ((\left(\pm 1 \right))^(3))+1\cdot 0-2\cdot 0=0 \\& \pm 1+0-0=0 \\& \pm 1=0 \\\end(align) Hence, cosx=0\cos x=0 is not a solution. We have proven that cosx≠0\cos x\ne 0. Now that we have proven this, let's divide our original equation by cos3
x((\cos )^(3))x. Why in a cube? Because we just proved that our original equation has the third power:
sin3
xcos3
x+sin2
xcosxcos3
x−2=0
t g3
x+t g2
x−2=0 \begin(align)& \frac(((\sin )^(3))x)(((\cos )^(3))x)+\frac(((\sin )^(2))x\ cos x)(((\cos )^(3))x)-2=0 \\& t((g)^(3))x+t((g)^(2))x-2=0 \\\end(align) Let's introduce a new variable: tgx=t Let's rewrite the construction: t3
+t2
−2=0
((t)^(3))+((t)^(2))-2=0 We have a cubic equation. How to solve it? Initially, when I was just putting together this video tutorial, I planned to first talk about factoring polynomials and other techniques. But in this case everything is much simpler. Take a look at our given identity, with the term with the highest degree worth 1. In addition, all coefficients are integers. This means that we can use a corollary from Bezout’s theorem, which states that all roots are divisors of the number -2, i.e. the free term. The question arises: what is -2 divided by? Since 2 is a prime number, there are not many options. These can be the following numbers: 1; 2; -1; -2. Negative roots immediately disappear. Why? Because both of them are greater than 0 in absolute value, therefore t3
((t)^(3)) will be greater in modulus than t2
((t)^(2)). And since the cube is an odd function, therefore the number in the cube will be negative, and t2
((t)^(2)) - positive, and this whole construction, with t=−1 t=-1 and t=−2 t=-2, will not be more than 0. Subtract -2 from it and get a number that is certainly less than 0. Only 1 and 2 remain. Let’s substitute each of these numbers: ˜
t=1→ 1+1−2=0→0=0 ˜t=1\to \text( )1+1-2=0\to 0=0 We have obtained the correct numerical equality. Hence, t=1 t=1 is the root. t=2→8+4−2=0→10≠0 t=2\to 8+4-2=0\to 10\ne 0 t=2 t=2 is not a root. According to the corollary and the same Bezout’s theorem, any polynomial whose root is x0
((x)_(0)), represent it in the form: Q(x)=(x= x0
)P(x) Q(x)=(x=((x)_(0)))P(x) In our case, in the role x x acts as a variable t t, and in the role x0
((x)_(0)) is a root equal to 1. We get: t3
+t2
−2=(t−1)⋅P(t) ((t)^(3))+((t)^(2))-2=(t-1)\cdot P(t) How to find a polynomial P (t) P\left(t\right)? Obviously, you need to do the following: P(t)= t3
+t2
−2
t−1 P(t)=\frac(((t)^(3))+((t)^(2))-2)(t-1) Let's substitute: t3
+t2
+0⋅t−2t−1=t2
+2t+2 \frac(((t)^(3))+((t)^(2))+0\cdot t-2)(t-1)=((t)^(2))+2t+2 So, our original polynomial is divided without a remainder. Thus, we can rewrite our original equality as: (t−1)( t2
+2t+2)=0 (t-1)(((t)^(2))+2t+2)=0 The product is zero when at least one of the factors is zero. We have already considered the first multiplier. Let's look at the second one: t2
+2t+2=0 ((t)^(2))+2t+2=0 Experienced students have probably already realized that this construction has no roots, but let’s still calculate the discriminant. D=4−4⋅2=4−8=−4 D=4-4\cdot 2=4-8=-4 The discriminant is less than 0, therefore the expression has no roots. In total, the huge construction was reduced to the usual equality: \[\begin(array)(·(35)(l)) t=\text( )1 \\tgx=\text( )1 \\x=\frac(\text( )\!\!\pi\!\!\text( ))(4)+\text( ) \!\!\pi\!\!\text( )k,k\in Z \\\end(array)\] In conclusion, I would like to add a couple of comments on the last task: Homogeneous trigonometric equations are a favorite topic in all kinds of tests. They can be solved very simply - just practice once. To make it clear what we are talking about, let’s introduce a new definition. A homogeneous trigonometric equation is one in which each non-zero term consists of the same number of trigonometric factors. These can be sines, cosines, or combinations thereof - the solution method is always the same. The degree of a homogeneous trigonometric equation is the number of trigonometric factors included in the non-zero terms. Examples: sinx+15 cos x=0 \sin x+15\text( cos )x=0 - identity of the 1st degree; 2 sin2x+5sinxcosx−8cos2x=0 2\text( sin)2x+5\sin xcosx-8\cos 2x=0 - 2nd degree; sin3x+2sinxcos2x=0 \sin 3x+2\sin x\cos 2x=0 - 3rd degree; sinx+cosx=1 \sin x+\cos x=1 - and this equation is not homogeneous, since there is a unit on the right - a non-zero term in which there are no trigonometric factors; sin2x+2sinx−3=0 \sin 2x+2\sin x-3=0 is also a non-homogeneous equation. Element sin2x\sin 2x is of the second degree (since it can be represented sin2x=2sinxcosx \sin 2x=2\sin x\cos x), 2sinx 2\sin x is the first one, and the term 3 is generally zero, since there are no sines or cosines in it. The solution scheme is always the same: Let's assume that cosx=0\cos x=0. Then sinx=±1\sin x=\pm 1 - this follows from the main identity. Let's substitute sinx\sin x and cosx\cos x into the original expression, and if the result is nonsense (for example, the expression 5=0
5=0), go to the second point; We divide everything by the power of the cosine: cosx, cos2x, cos3x... - depends on the power value of the equation. We obtain the usual equality with tangents, which can be safely solved after replacing tgx=t.
tgx=tThe roots found will be the answer to the original expression. State budgetary professional educational institution in the village of Teeli of the Republic of Tyva Development of a lesson in mathematics Lesson topic: "Homogeneous trigonometric equations" Teacher: Oorzhak Ailana Mikhailovna Lesson topic : “Homogeneous trigonometric equations”(according to the textbook by A.G. Mordkovich) Group : Master of Plant Growing, 1st year Lesson type: A lesson in learning new material. Lesson objectives: 2. Develop logical thinking, the ability to draw conclusions, the ability to evaluate the results of actions performed 3. To instill in students accuracy, a sense of responsibility, and the development of positive motives for learning Lesson equipment:
laptop, projector, screen, cards, posters on trigonometry: meanings of trigonometric functions, basic trigonometry formulas. Lesson duration: 45 minutes. Lesson structure: Structural element of the lesson front (min) Methodological features, brief instructions for conducting the lesson stage Teacher's activities Student activities Organizational moment Control of student attendance. α
0
The teacher checks readiness for the lesson The attendants report those absent from class Updating of reference knowledge Checking homework α 2 Repetition of basic concepts Makes his rounds 3 students write down the solution at the board. The rest do mutual checking Formation of new knowledge Motivational moment α 2 Examples of trigonometric equations on the screen Asks questions Answer Explanation of a new topic α 1 On the screen are slides with the solution of homogeneous trigonometric equations The teacher explains the topic Students listen and write down Consolidation Solving Examples α 2 Weak students work with the teacher. Strong students work independently. Works with weak students at the board. Solve examples Differentiated independent work α 2 Hand out cards Makes a round. Control of weak students Solve examples Summing up α 1 Summing up the lesson. Communicating grades to students The teacher summarizes and reports grades Students listen Issuing homework α 1 Tell students homework The teacher gives brief instructions on homework Write down homework Progress of the lesson. 1. Organizational moment (1 min) Check the readiness of students for the lesson, listen to the group on duty. 2. Updating basic knowledge (3 min) 2.1. Checking homework. Three students solve at the board No. 18.8 (c, d); No. 18.19. The rest of the students do a peer review. No. 18.8 (c) 5 cos 2 x + 6 sin x – 6 = 0 5 (1 - sin x) + 6 sin x – 6 = 0 5 - 5 sin 2 x + 6 sin x – 6 = 0 5 sin 2 x + 6 sin x – 1 = 0 5 sin 2 x – 6 sin x + 1 = 0 z=sin x, 5z 2 – 6 z + 1 = 0 z 1 = 1, sin x = 1, x= +2 π n, n Z z 2 = , sin x = , x= (-1) n arcsin + π n, n Z Answer: x= +2 π n, x=(-1) n arcsin + π n, n Z No. 18.8 (g) 4 sin 3x + cos 2 3x = 4 4 sin 3x + (1-sin 2 3x) – 4 = 0 Sin 2 3x + 4 sin 3x – 3 = 0 sin 2 3x – 4 sin 3x + 3 = 0 z=sin 3x, z 2 – 4 z + 3 = 0 z 1 = 3, does not satisfy the condition z 2 = 1, sin 3x =1, 3х= +2 π n, n Z X = + π n , n Z Answer: x = + π n, n Z No. 18.19 (c) сos = 2x – = , n Z x 1 = , n Z x 2 = , n Z a) b) 0, , , c) - d) - , 0, 3. Learning new material (13 min) 3.1. Motivation of students. Students are asked to name equations that they know and can solve (slide No. 1) 1) 3 cos 2 x – 3 cos x = 0; 2) cos (x – 1) = ; 3) 2 sin 2 x + 3 sin x = 0; 4) 6 sin 2 x – 5 cos x + 5 = 0; 1 2 5) sin x cos x + cos²x = 0; 6) tg + 3ctg = 4. 7) 2sin x – 3cos x = 0; 8) sin 2 x + cos 2 x = 0; 9) sin²х – 3sinх cos x+2cos²х = 0. Students will not be able to name the solution to equations 7-9. 3.2. Explanation of a new topic. Teacher: Equations that you could not solve are quite common in practice. They are called homogeneous trigonometric equations. Write down the topic of the lesson: “Homogeneous trigonometric equations.” (slide number 2) Determination of homogeneous equations on the projector screen. (slide number 3) Consider a method for solving homogeneous trigonometric equations (slide No. 4, 5) I degree II degree a sinx + b cosx = 0, (a,b ≠ 0). Let's divide both sides of the equation term by term by cosx ≠ 0. We get: a tgx + b = 0 Tgx = - – simplest trigonometric equation a sin²x + b sinx cosx + c cos²x = 0. 1) if a ≠ 0, divide both sides of the equation term by term by cos²x ≠0 We get: a tg²x + b tgx + c = 0, solve by introducing a new variable z= tgx 2) if a = 0, then We get: b sinx cosx + c cos²x =0, solve by factorization method When dividing a homogeneous equation a sinx + b cosx = 0 at cos x ≠ 0 When dividing a homogeneous equation a sin²x + b sinx cosx + c cos²x = 0 by cos 2 x ≠ 0 the roots of this equation are not lost. Analyze the solutions to the examples Example 1. Solve equation 2sin x – 3cos x = 0; (slide number 6) This is a homogeneous equation of the first degree. Let's divide both sides of the equation term by cos x , we get: 2tg x – 3 = 0 tg x = x = arctan + πn , n Z. Answer: x = arctan + π n, n Z. Example 2 . Solve sin 2 equation x + cos 2 x = 0; (slide number 7) This is a homogeneous equation of the first degree. Let's divide both sides of the equation term by cos 2 x , we get: tg2 x + 1 = 0 tg2 x = - 1 2x = arctan (-1)+ πn, n Z. 2x = - + πn, n Z. x = - + , n Z. Answer: x = - + , n Z. Example 3 . Solve the equation sin²х – 3sinх cos x+2cos²х = 0. (slide number 8) Each term in the equation has the same degree. This is a homogeneous equation of the second degree. Let's divide both sides of the equation term by term by cos 2 x ≠ 0, we get: tg 2 x-3tg x+2 = 0. Let's introduce a new variable z = tan x, we get z 2 – 3z + 2 =0 z 1 = 1, z 2 = 2 this means either tg x = 1 or tg x = 2 tan x = 1 x = arctan 1 + πn, n Z x = + πn, n Z tan x = 2 x = arctan 2 + πn, n Z Answer: x = + πn, x = arctan 2 + πn, n Z 4. Consolidation of the studied material (10 min) The teacher analyzes in detail examples with weak students on the board, strong students solve independently in their notebooks. No. 18.12 (a) 18.24 (a) 18.24 (b) sin 2 x + 2 sin x cos x – 3 cos² x = 0 tg 2 x + 2 tg x – 3 = 0 z = tan x z 2 + 2 z – 3 = 0 z 1 = 3; z 2 = - 1. tan x = 3, x = arctan 3 + πn, n Z tan x = -1, x = arctan (-1) + πn, n Z x = + πn, n Z Answer: x = arctan 3 + πn, X = + πn, n Z sin 2 x = cos 2 x tg2x = 1 2x = arctan 1 + πn, n Z 2x = + πn, n Z x = + , n Z Answer: x = + , n Z Tg 3 x = 1 tg 3 x = 3 x = + πn, n Z x = + , n Z 5. Differentiated independent work (15 min) The teacher issues cards with tasks of three levels: basic (A), intermediate (B), advanced (C). Students themselves choose which level of examples they will solve. Level A 2 sin x+ 2 cos x = 0 cos x+ 2 sin x = 0 Level B 2 sin x+ 2 cos x = 0 6 sin 2 x - 5 sinx cos x + cos 2 x =0 Level C 5 sin 2 x + 2 sinx cos x - cos 2 x =1 2 sin x - 5 cos x = 3 1- 4 sin 2x + 6 cos 2 x = 0 6. Summing up. Reflection on learning activities in the lesson (2 min) Answer the questions: What types of trigonometric equations have we learned? How to solve a homogeneous equation of the first degree? How to solve a homogeneous equation of the second degree? I found out... I learned... Recognize the good work of individual students in the lesson and give grades. 7. Homework. (1 min) Inform students of their homework and give brief instructions on how to complete it. No. 18.12 (c, d), No. 18.24 (c, d), No. 18.27 (a) Used literature: "Homogeneous trigonometric equations" 1. An equation of the form a sin x + b cos x = 0, where a ≠0, b ≠0 is called a homogeneous trigonometric equation of the first degree. 2. An equation of the form a sin 2 x + b sin x cos x + c cos 2 x = 0, where a ≠0, b ≠0, c ≠0 is called a homogeneous trigonometric equation of the second degree. Definition: I degree a sinx + b cosx = 0, (a,b ≠ 0). Let's divide both sides of the equation term by term by cosx ≠ 0. We get: a tanx + b = 0 tgx = -b /a the simplest trigonometric equation When dividing a homogeneous equation a sinx + b cosx = 0 by cos x ≠ 0, the roots of this equation are not lost. Method for solving homogeneous trigonometric equations a sin²x + b sinx cosx + c cos²x = 0. 1) if a ≠ 0, divide both sides of the equation term by cos ² x ≠0 We obtain: a tan ² x + b tanx + c = 0, solve by introducing a new variable z = tgx 2) if a = 0, then we get: b sinx cosx + c cos ² x =0, solve by factorization method / When dividing the homogeneous equation a sin ² x + b sinx cosx + c cos ² x = 0 by cos 2 x ≠ 0 the roots of this equation are not lost. II degree This is a homogeneous equation of the first degree. Let's divide both sides of the equation term by term by cos x, we get: Example 1. Solve the equation 2 sin x – 3 cos x = 0 This is a homogeneous equation of the first degree. Let's divide both sides of the equation term by cos 2 x, we get: Example 2. Solve the equation sin 2 x + cos 2 x = 0 Each term in the equation has the same degree. This is a homogeneous equation of the second degree. Let's divide both sides of the equation term by term with os 2 x ≠ 0, we get: Example 3. Solve the equation sin ² x – 3 sin x cos x+2 cos ² x = 0 Answer the questions: - What types of trigonometric equations have we studied? -How to solve a homogeneous equation of the first degree? - How to solve a homogeneous equation of the second degree? Summing up I learned... - I learned... Reflection No. 18.12 (c, d), No. 18.24 (c, d), No. 18.27 (a) Homework. Thanks for the lesson! Well done! Self-analysis of a mathematics lesson by teacher Oorzhak A.M. Group : Master of Plant Growing, 1st year. Lesson topic : Homogeneous trigonometric equations. Lesson type : A lesson in learning new material. Lesson objectives: 1. To develop students’ skills in solving homogeneous trigonometric equations, to consider methods for solving homogeneous equations of basic and advanced levels of complexity. 2. Develop logical thinking, the ability to draw conclusions, and the ability to evaluate the results of actions performed. 3. To instill in students accuracy, a sense of responsibility, and the development of positive motives for learning. The lesson was conducted according to thematic planning. The topic of the lesson reflects the theoretical and practical parts of the lesson and is understandable to students. All stages of the lesson were aimed at achieving these goals, taking into account the characteristics of the group. Lesson structure. 1. The organizational moment included the preliminary organization of the group, the mobilizing beginning of the lesson, the creation of psychological comfort and the preparation of students for the active and conscious assimilation of new material. The preparation of the group and each student was checked visually by me. Didactic task of the stage: Ppositive attitude towards the lesson. 2. The next stage is updating the students’ basic knowledge. The main task of this stage is: restoration in the students’ memory of the knowledge necessary for learning new material. The updating was carried out in the form of checking homework at the board. 3. (Main stage of the lesson) Formation of new knowledge. At this stage, the following didactic tasks were implemented: Ensuring perception, comprehension and primary memorization of knowledge and methods of action, connections and relationships in the object of study. This was facilitated by: the creation of a problem situation, the method of conversation in combination with the use of ICT. An indicator of the effectiveness of students’ assimilation of new knowledge is the correctness of answers, independent work, and active participation of students in work. 4.The next stage is the primary consolidation of the material. The purpose of which is to establish feedback to obtain information about the degree of understanding of the new material, completeness, correctness of its assimilation and for timely correction of detected errors. For this I used: solving simple homogeneous trigonometric equations. Here, tasks from the textbook were used that correspond to the required learning outcomes. The initial consolidation of the material was carried out in an atmosphere of goodwill and cooperation. At this stage, I worked with weak students, the rest decided on their own, followed by self-testing from the board. 5. The next moment of the lesson was the primary control of knowledge. Didactic task of the stage: Identifying the quality and level of mastery of knowledge and methods of action, ensuring their correction. Here, she implemented a differentiated approach to learning and offered the children a choice of tasks of three levels: basic (A), intermediate (B), and advanced (C). I made a round and noted the students who chose the basic level. These students performed the work under the supervision of the teacher. 6. At the next stage - summing up, the tasks of analyzing and assessing the success of achieving the goal were solved. Summing up the lesson, I simultaneously reflected on the learning activity. Students learned ways to solve homogeneous trigonometric equations. Grades were given. 7. The final stage is homework. Didactic task: Ensuring students understand the content and methods of completing homework. Gave brief instructions on how to do homework. During the lesson, I was able to realize teaching, developmental and educational goals. I think that this was facilitated by the fact that from the first minutes of the lesson the children showed activity. They were ready to accept a new topic. The atmosphere in the group was psychologically favorable.Solution algorithm
Let's select the terms
We use the formula of the main trigonometric identity and write down the final solution
We solve real problems
Task No. 1
Task No. 2
Task No. 3
Key Points
General solution scheme
Slide 2
Preview:
